Про парадоксы

Парадоксы, парадоксы, парадоксы … «ПАРАДОКС (от греч. παραδοξος — неожиданный, странный), то же, что и противоречие; <…> В логике П. (или антиномиями, противоречиями) наз. высказывания, в точном смысле слова противоречащие логическим законам:» [1, с. 477]. «Парадокс в более узком и гораздо в более современном значении — это два противоположных утверждения, для каждого из которых имеются представляющиеся убедительными аргументы» [2, с. 158]. Иными словами, допускается существование высказываний-утверждений, которые являются истинными и ложными одновременно, что никоим образом не согласуется с логическим законом противоречия: «ПРОТИВОРЕЧИЯ ПРИНЦИП, закон противоречия, принцип (закон) непротивречия, принцип отрицания (запрещения, недопустимости) противоречия, основной логич. закон, согласно к-рому никакое высказывание (предложение, суждение) и его отрицание не могут одновременно быть истинными;» [1, с. 546], таким образом, допуская существование подобных высказываний, мы обязаны отказаться от закона противоречия, либо, считая закон противоречия универсальным законом логики, выдвинуть, как его следствие, тезис: парадоксов нет, есть только ошибки, приводящие к противоречиям.

Парадокс “близнецы”. Всем хороша теория относительности Эйнштейна: и идея интересная, и уравнения — просто загляденье. Вот только в рамках СТО обнаружился парадокс “близнецы”, который основан на утверждении, что с увеличением скорости объекта для него замедляется время. Физики-теоретики решили отмахнуться от этого парадокса: “мол, мы не знаем, как течет время при разгоне и торможении объекта”. Так ведь крайне необходимо решить этот вопрос для того, чтобы избавить СТО от ярлыка противоречивости. Кроме того, К. Гёдель доказал, что в рамках общей теории относительности время может быть закольцовано, т.е. возможны путешествия во времени: «В этих статьях он описал семейство космологических решений уравнений Эйнштейна, обладающее целым рядом новых свойств. Наиболее удивительные из них — наличие замкнутых временных кривых в его исходной нерасширяющейся модели. Таким образом, в этой модели наблюдатель, в принципе, мог бы путешествовать в собственное прошлое» [3, с. 228]. Физики-теоретики опять решили отмахнуться: “мол, это возможно только в теории, а в действительности этого быть не может”. Тогда возникает резонный вопрос: “Для чего нужна теория, которая описывает то, чего быть не может?”.

Парадокс Даламбера (Д’Аламбера). После того, как Даниил Бернулли опубликовал свой труд «Гидродинамика» [4] поднялся шквал критики, указывающей на многочисленные противоречия. Даламбер даже опубликовал работу, в которой он указал на парадокс, возникающий в рамках основного закона гидродинамики, открытого Д. Бернулли. Парадокс заключается в том, что круглое тело, помещенное в поток идеальной жидкости (идеальная жидкость — жидкость без вязкости), не испытывает сопротивления. И здесь, специалисты по гидродинамике решили отмахнуться: “в реальности идеальной жидкости не существует, а в вязкой жидкости этот парадокс не возникает”. Но дело вовсе не в вязкости, а в том, что закон Д. Бернулли в корне противоречит законам Ньютона, в соответствии с которыми, только приложенная к телу сила может изменить значение и/или направление его движения.

Парадокс Галилея. «В 1638 г. Галилей отметил «парадокс», состоящий в том, что между квадратами целых положительных чисел и самими целыми положительными числами можно установить 1—1-соответствие, а это вступает в противоречие с евклидовой аксиомой, согласно которой целое больше любой из своих собственных частей (собственная часть — это часть, не совпадающая со всем целым)» [5, с. 207].

О факте, что между элементами множества квадратов натуральных чисел и множеством самих натуральных чисел можно установить взаимно однозначное соответствия, необходимо указать на предупреждение Больцано о недопустимости такого соответствия в качестве меры сравнения бесконечных множеств: «<…> на одном только этом основании невозможно еще заключить, как видим, что эти оба  многообразия,  если  они  бесконечны  равны  друг  другу в отношении множества своих частей (т.е. если мы не примем во внимание никаких других различий между частями)» [6, с.32].

Действительно, на том основании, что между точками любых двух разных отрезков можно установить взаимно однозначное соответствие, наивно полагать все отрезки равными. Поэтому, Больцано предлагал найти дополнительную характеристику, позволяющую сравнивать бесконечные множества, аналогичную длине отрезков: «О равенстве этих множеств можно будет заключить только тогда, когда для этого будет существовать еще какое-нибудь другое основание, как, например, то, что оба многообразия имеют совершенно одинаковые определяющие их основания, например, совершенно одинаковое происхождение» [6, с. 32]. В качестве основы меры сравнения бесконечных множеств чисел можно, например, использовать понятие плотности распределения чисел на действительной оси. Тогда видим, что четные натуральные числа встречаются на этой оси в два раза реже, чем все натуральные числа (рис. 1).

Тогда можно говорить, что объем множества четных чисел в два раза меньше объема множества всех натуральных чисел [7].

Парадокс Бертрана. Теория вероятностей, казалось бы “молодая зеленая ветвь” математики, но настолько изъедена парадоксами [8], что являет собой “трухлявый пень” — пни и развалится. Такое обилие парадоксов позволяет называть теорию вероятностей теорией “Чего изволите?”. Пример? Пожалуйста! Парадокс Бертрана: «Требуется определить вероятность того, что взятая произвольно хорда окружности будет больше, чем сторона вписанного в нее равностороннего треугольника.

По-разному понимая слова “взятая произвольно”, мы будем получать разные вероятности. Так, рассматривая только те хорды, которые параллельны данному направлению, мы получим, что искомая вероятность равна ½. Действительно, в этом случае хорды, большие, чем сторона треугольника, будут находиться от центра на расстоянии, меньшем r/2 (рис. 2).

Если считать, что произвольно проведенные хорды будут выходить из определенной точки на окружности, то искомая вероятность равна ¹/₃ (рис.3). Если мы будем считать, что слова “взятая произвольно” означают, что вероятность попадания середины хорды внутрь какой-либо части круга пропорциональна площади этой части, то получим, что искомая вероятность равна ¼. Действительно, так как серединой хорды может быть любая точка круга, а середины хорд, которые больше стороны треугольника, заполняют круг радиуса r/2, то искомая вероятность будет π(r/2)²/πr²=¼ (рис. 4).

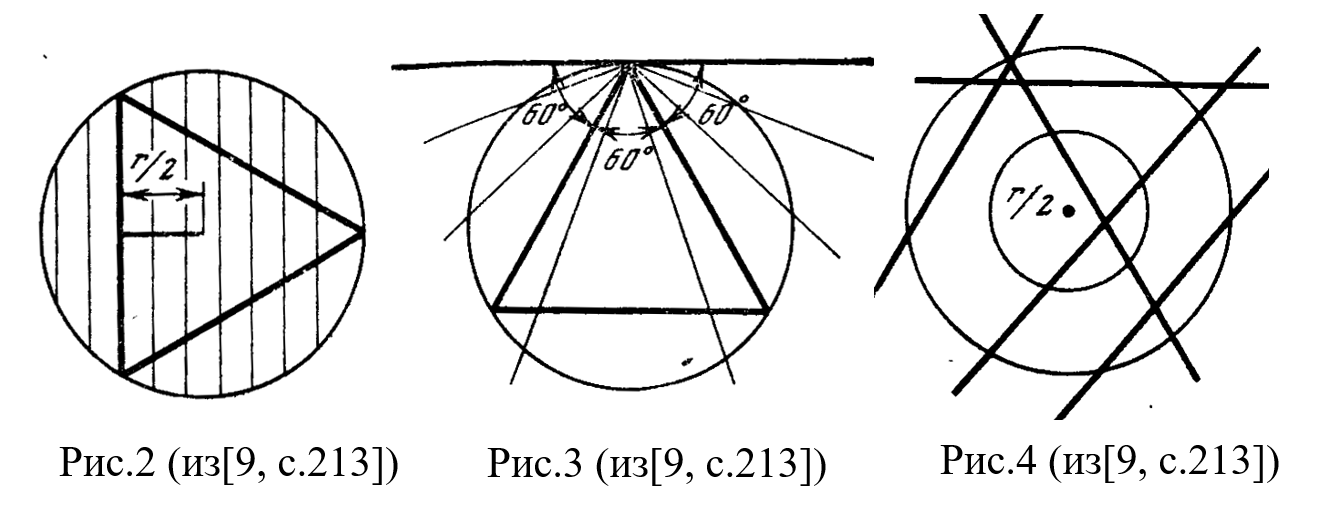
При других трактовках «произвольного взятия» можно получить и другие вероятности» [9, с. 212-213]. Вот только вне зависимости от понимания “произвольно взятая”, во всех трех вариантах центры хорд, превосходящих сторону правильного треугольника, вписанного в окружность, находятся внутри вписанного круга (рис. 5).

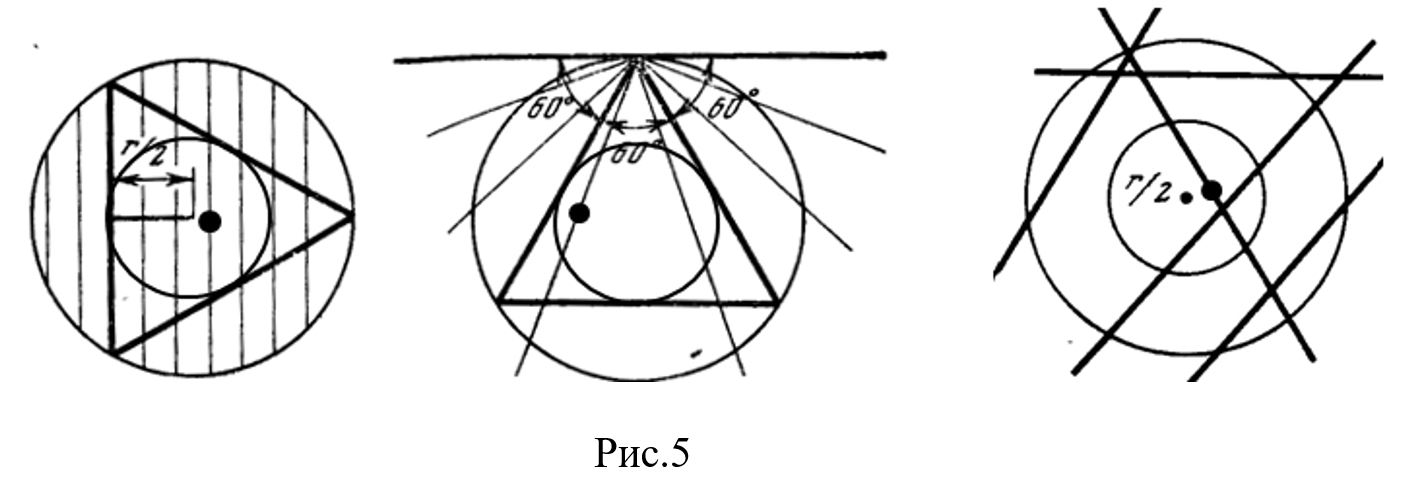
Таким образом, получаем, что 1/2=1/4 и 1/3=1/4. А из этого может следовать все что угодно, т.е. “Чего изволите?”. Хотя, правильный ответ, исходя из определения хорды, равен 1/3.

Еще большее удивление вызывает парадокс независимости: «Предположим, что бросают две правильные монеты. Пусть событие A – «на первой монете выпал герб», событие B – «на второй монете выпал герб» и событие C – «на одной (и только на одной) монете выпал герб». Тогда события A, B и C попарно независимы, но любые два из них однозначно определяют третье» [8, с. 23]. О какой зависимости может идти речь? Ведь изначально определяется, что объектами теории вероятностей являются случайные события, исходы которых зависят только от случая. Как же тогда можно говорить о том, что случайные события зависят друг от друга?

Апория Зенона “Дихотомия”. «А. «Дихотомия» (разделение на два): прежде чем пройти весь путь, движущееся тело должно пройти половину этого пути, а ещё до этого – четверть и т.д.; поскольку процесс такого деления бесконечен, то тело вообще не может начать двигаться (или движение не может окончиться)» [1, с. 31]. Со временем эта апория (затруднение) проникла в математику, точнее, в теорию множеств, но уже в качестве строгого научного способа доказательства. Рассмотрим множество действительных чисел на интервале от 0 до 1 (числа 0 и 1 не входят в это множество). Эти числа являют собой упорядоченную последовательность, т.е. каждое число d_i имеет как предыдущее, так и последующее число (. . . <d_i-2<d_i-1<d_i<d_i+1<d_i+2< . . .). Применяя метод деления пополам к этому интервалу будем получать все меньшие и меньшие интервалы: (0;1), (0;1/2), (0;1/4), (0;1/8) и т.д. В связи с потенциальной бесконечностью данного процесса, утверждают, что на этом интервале нет наименьшего действительного числа d_min. Но такое число должно быть, его не может не быть! Если нет числа, которое непосредственно следует за числом нуль, то нет и никаких других действительных чисел, а есть только натуральные числа. Для того чтобы убедиться в существовании числа d_min, достаточно рассмотреть множество действительных чисел на интервале от -1/2 до +1/2. Тогда число 0 является рядовым числом в упорядоченной последовательности. Обозначив число 0 как d₀, получим . . . <d_-2<d_-1<d₀<d₁<d₂< . . . Число d₁ и является наименьшим числом множества действительных чисел на интервале (0;1). Этому числу можно присвоить номер 1, следующему за ним — номер 2 и т.д. Следовательно, множество действительных чисел является счетным. Учитывая тот факт, что каждому действительному числу на действительной оси соответствует одна и только одна точка, приходим к решению апории Зенона «Дихотомия»: при движении, тело из начальной точки попадает в следующую за ней точку, из этой точки — в следующую за ней точку и т.д. до конечной точки своего движения.

Парадокс Рассела. «В 1902 г. Бертран Рассел поразил философов и математиков, указав антиномию (см. § 2), относящуюся к самым началам теории множеств и показывающую, что в основаниях этой дисциплины что-то неблагополучно. Но антиномия Рассела потрясла основы не только теории множеств: в опасности оказалась и сама логика. Требовалось лишь легкое изменение в формулировке, чтобы перевести антиномию Рассела в противоречие, которое можно было бы сформулировать в терминах самых основных логических понятий» [10, с. 12].

Клайн писал: «<…> обнаруженное противоречие ставит под удар само понятие множества, или класса объектов, широко используемое во всей математике. По словам Гильберта, парадокс Рассела был воспринят математическим миром как катастрофа» [11, с. 238-239].

Парадокс Рассела состоит в следующем: «Для произвольного данного множества представляется вполне осмысленным выяснить, является оно своим собственным элементом или нет. По отношению к некоторым множествам трудно усомниться в том, что они не являются собственными элементами: множество планет, например, не является, конечно, планетой и потому не есть собственный элемент. Другие множества столь же естественно без колебаний считать собственными элементами: очевидный пример — множество всех множеств. Поэтому кажется вполне осмысленным поставить тот же вопрос относительно множества всех множеств, не являющихся собственными элементами. Ответ на этот вопрос, однако, обескураживает: обозначив последнее множество через 'S', мы сразу видим, что если S есть элемент S, то оно принадлежит множеству всех множеств, не являющихся собственными элементами, т. е. оно не есть собственный элемент; с другой стороны, если S не есть элемент S, оно не принадлежит множеству всех множеств, не являющихся собственными элементами, а потому является собственным элементом. Сопоставляя сказанное, мы убеждаемся, что S есть элемент S в том и только в том случае, когда S не есть элемент S, — явное противоречие, выведенное из весьма правдоподобных предположений цепью бесспорных на вид рассуждений» [10, с. 16-17].

По поводу этого парадокса следует напомнить поговорку: «Не так страшен Черт, как его малюют». В действительности же парадокс Б. Рассела парадоксом не является [12]. Фактически это стандартное доказательство от противного того факта, что нет множеств, содержащих себя в качестве собственного элемента. Сформулируем и назовем в честь Б. Рассела следующую теорему:

Теорема Рассела. Не существуют множества, содержащие себя в качестве собственного элемента.

Доказательство. Доказательство проведем от противного. Предположим, что такие множества существуют. Тогда, следуя рассуждениям Рассела, приходим к парадоксу Рассела, т.е. получаем противоречие. Что и требовалось доказать.

Таким образом, в парадоксе Рассела проявилась третья — доказующая ипостась парадоксов [13]. Если же кто-нибудь пожелает привести пример множества, содержащего себя в качестве собственного элемента, пусть найдет ошибку в рассуждениях Рассела.

Парадоксы, парадоксы, парадоксы . . . «И куда только смотрит Комиссия РАН по борьбе с лже-наукой?! » [14, с. 9].

1. Философский энциклопедический словарь. — М.: Сов. Энциклопедия, 1983. — 840 с.
2. Ивин А.А. По законам логики. — М.: Молодая гвардия, 1983. — 208 с., ил. — (Эврика).
3. Крайзель Г. Биография Курта Гёделя. //Успехи математических наук. 1988, т. 43, вып. 2(260), с. 175-238.
4. Д. Бернулли. Гидродинамика, или записки о силах и движениях жидкостей. Издательство АН СССР. 1959. 552 с.
5. Клини С. К. Математическая логика. – М.: Мир. – 1973, 480 с.
6. Больцано Б. Парадоксы безконечнаго. – Одесса. – 1911, 112 с.
7. Черкасов М. Ю. О парадоксе Галилея. – // Наука сегодня: теория и практика [Текст]: Материалы международной научно-
8. Секей Г. Парадоксы в теории вероятностей и математической статистике: Пер. с англ. — М.: Мир, 1990. — 240 с. ил.
9. Майстров Л. В. Развитие понятия вероятности. М.: Наука. 1980. 156 с.
10. Френкель Α. Α., Бар-Хиллел И. Основания теории множеств. /Пер. с англ. Ю.А. Гастева под ред. А.С. Есенина-Вольпина. — М.: Мир, 1966, — 556 с.
11. Клайн М. Математика. Утрата определенности. /Пер. с англ. Ю.А. Данилова под ред. д-ра физ.-мат. наук, проф. И.М. Яглома. — М.: Мир, 1984, — 423 с.
12. Черкасов М. Ю. Парадокс Рассела — парадокс ли? (http://www.twirpx.org/file/2570818/).
13. Черкасов М. Ю. О логических парадоксах. (http://www.twirpx.org/file/1634404/).
14. Зенкин А. А. Трансфинитный рай Георга Кантора. //Альманах «Мысли об Истине». 2017. № 115, 124 с.