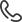Исследование условий вырожденности квадратных матриц, составленных из последовательных членов арифметических прогрессий

1. Анализ состояния проблемы исследования, отражающий актуальность темы работы

 

Исследователями отмечается, что формирование научно-исследователь­ской работы студентов (НИРС) должно происходить в учебном процессе с самых первых занятий и стать одним из важных направлений подготовки бакалавров ([1]). Без соответствующего опыта, знаний, умений и мотивов в области исследовательской деятельности обучающиеся не смогут проводить научные изыскания ([2]).

С первых занятий научным руководителем перед студентами ставились проблемные учебные задачи. В качестве примера рассмотрим решение одной из учебных задач, поставленных научным руководителем перед обучающимися.

Во время изучения нескольких взаимосвязанных тем по (дисциплина «Математика» 1-й курс) изучению матриц, определителей и решения систем линейных уравнений вычисление одного из определителей привело к неожиданным результатам. В качестве элементов определителя выступали коэффициенты системы линейных уравнений, которые представляли собой члены прогрессирующих последовательностей, в частности, арифметических и геометрических прогрессий. Члены указанных прогрессий, последовательно записанные в квадратные матрицы различных порядков, обладают свойством: определители указанных матриц равны 0.

Поиск по литературным источникам, среди которых литература из рабочей программы по математике, а также такие источники, как «Введение в теорию матриц» Р.Беллман [3], «Курс высшей алгебры» А.Г.Курош [4], показывает, что указанный выше результат ни в одном из источников не представлен. Поэтому изучение вопроса о прогрессирующих последовательностях и квадратных матрицах (и их определителях), составленных из последовательных членов последовательностей, является актуальным.

 

2. Постановка проблемы исследования и вытекающие из неё задачи

 

Сама идея исследования возникла во время обсуждения некоторых свойств систем линейных уравнений во время лекционного занятия по математике. Нужно было записать матрицу, определитель которой отличен от нуля. В квадратную матрицу были занесены последовательные натуральные числа, преподаватель в среде MathCAD вычислил определитель – его значение оказалось нулевым!

Изменения в одной из строк – поменялись элементы 1 и 3 во второй строке, а, затем, и вовсе во 2-й строке (аналогично и 2-м столбце) записаны члены убывающей арифметической прогрессии с отрицательными членами, привели к тому, что определитель матрицы по-прежнему давал значение нуль. Более того, вместо членов арифметической прогрессии были подставлены члены геометрической прогрессии и вновь определитель получился нулевым (само по себе это не удивительно – элементы строк пропорциональны!). Но для членов арифметической прогрессии пропорциональности в явном виде не наблюдается. Но автору и его научному руководителю удалось обнаружить причины вырожденности квадратных матриц, составленных из членов одной и той же арифметической прогрессии.

Появляется вопрос: как поведёт себя квадратная матрица размерностью больше двух, если её заполнять элементами различных последовательностей. Таким образом, проблема состоит в следующем: установление свойства вырожденности квадратных матриц, составленных из последовательных элементов различных последовательностей.

Были поставлены цели и задачи: выявить свойства прогрессирующих последовательностей; определить класс последовательностей, обладающих аналогичными свойствами; определить значимость найденных свойств, их применения.

 

3. Характеристика объектов и методов исследования

 

Объектами исследования выступают числовые последовательности с заданными законами их получения, квадратные матрицы различных порядков, в которые заносятся последовательно члены последовательностей, их определители.

Предметом исследования являются свойства числовых последовательностей, а, именно, значения определителей, получаемых из последовательных членов числовых последовательностей.

Данное исследование проводилось с помощью математического пакета «MathCAD» с целью анализа и выявления свойств различных числовых последовательностей.

Для того чтобы провести данное исследование, необходимо владеть навыками интеллектуальной деятельности, уметь сопоставлять, обобщать, анализировать и делать самостоятельные выводы. Поэтому применены следующие методы исследования: анализ научно-методической литературы по теме, индукция и дедукция, анализ и синтез, сравнение, обобщение, эксперимент, в частности компьютерный эксперимент.

 

4. Результаты исследования во множестве вещественных чисел

 

Обсуждая во время лекционного занятия по математике некоторые свойства систем линейных уравнений, при вычислении основного определителя системы 3-х уравнений с тремя переменными был получен интересный результат. Вычисления определителей производились в среде MathCAD. Нужно было записать матрицу, определитель которой отличен от нуля (вырожденность или невырожденность предложенного преобразования, заданного системой линейных уравнений). Записав в матрицу первые девять чисел натурального ряда, преподаватель вычислил определитель – его значение оказалось нулевым (рисунок 1).

 

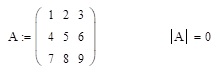
Рисунок 1 – Значение определителя матрицы

 

Изменение в одной из строк: поменялись элементы 1 и 3 во второй строке, а, затем, и вовсе во 2-й строке (аналогично и 2-м столбце) записаны члены убывающей арифметической прогрессии с отрицательными членами, ни к чему не привели: определитель матрицы по-прежнему давал значение нуль (рисунок 2).

 

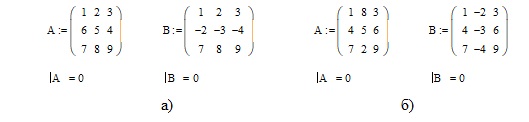
Рисунок 2 – Значение определителей матриц с изменениями:

а) во 2-й строке; б) во 2-м столбце

 

Автор данной работы заинтересовался полученными свойствами матриц, члены которых состоят из членов арифметических прогрессий. Был подготовлен обучающий интерактивный документ, в котором на примерах было показано вычисление определителей матриц, подготавливаемых указанным выше способом. Результаты были выложены в виде электронного документа, с которым могли ознакомиться все желающие – как преподаватели, так и студенты института. Некоторые из замечаний были учтены в обновляемом обучающем интерактивном документе [5].

 

4.1 Исследование вырожденности квадратных матриц, составленных из последовательных членов арифметических прогрессий

 

Учитывая, что ручной ввод различных наборов значений элементов матрицы значителен по времени для инициализации матриц была использована программа (функция пользователя) в среде MathCAD (рисунок 3) [5].

Поясним программу: происходит инициализация матрицы, в которой формируется линейный массив заданной длины (3-й параметр функции пользователя), переформируется с помощью вложенных циклов в двумерный квадратный массив с количеством строк и столбцов, вычисляемым с помощью отбрасывания дробной части корня квадратного из введенного пользователем числа, определяющего количество элементов в матрице, с целью предотвратить возможную ошибку (т.е. число – не квадрат натурального числа) при их вводе. Первый параметр – первый элемент арифметической прогрессии, второй – разность арифметической прогрессии.

Для того чтобы убедиться в выводе о том, что определитель, составленный из членов арифметических прогрессий, будет всегда равен нулю, достаточно в указанную программу вводить в функцию пользователя всякий раз различные значения. Указанная программа позволяет рассчитать определители и больших порядков (и с тем же результатом!) для членов арифметических прогрессий (рисунок 4).

 

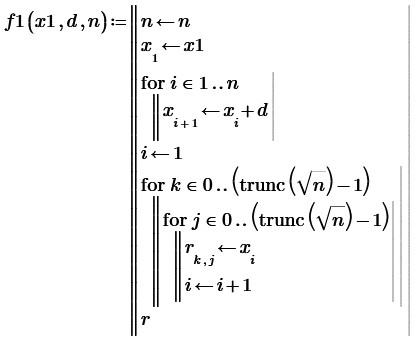
Рисунок 3 – Функция пользователя по заполнению матрицы элементами арифметической прогрессии

 

Рисунок 4 – Вычисление по программе (функция пользователя) определителя 5-го порядка для членов арифметической прогрессии

 

Проводя исследования с помощью MathCAD на множестве вещественных чисел, у нас возникла гипотеза 1.

Гипотеза 1. Определитель квадратной матрицы, заполненной произвольными, но последовательными членами одной или разных арифметических прогрессий для каждой строки (столбца), равен нулю.

 

4.1.1 Исследование вырожденности квадратных матриц третьего порядка, составленных из последовательных членов одной или разных арифметических прогрессий

 

1. Берем произвольную арифметическую прогрессию c первым элементом a₁ и разностью d. Составим квадратную матрицу третьего порядка из последовательных членов данной арифметической прогрессии.

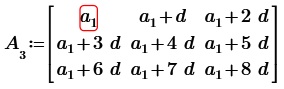
Пропорциональности строк или столбцов визуально не наблюдается. На основании свойств элементарных преобразований матриц вычтем из элементов второй и третьей строки соответствующие элементы первой строки, получим:

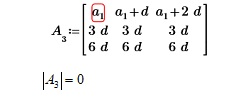
Наглядно видна пропорциональность второй и третьей строки, следовательно, определитель матрицы, составленный из элементов арифметической прогрессии, всегда равен 0.

Даже если поменяем первым и третий элементы любой строки, матрица тоже окажется вырожденной. Покажем на примере:

Поменяем в исходной матрице в третьей строке первый элемент с третьим местами, получим:

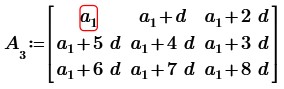
На основании свойств элементарных преобразований матриц вычтем из элементов второй и третьей строки соответствующие элементы первой строки, получим:

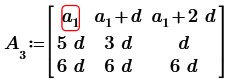
По свойству матриц транспонируем полученную матрицу:

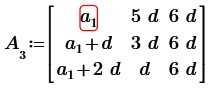
Вычтем из элементов второй и третьей строки соответствующие элементы первой строки:

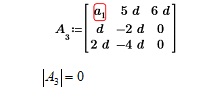
Тоже видна пропорциональность второй и третьей строки, следовательно, определитель матрицы, составленный из членов арифметической прогрессии, всегда равен 0.

2. Пойдем дальше: составим матрицу 3-его порядка из разных арифметических прогрессий, т.е. в каждой новой строке (или столбце) будет записана новая арифметическая прогрессия.

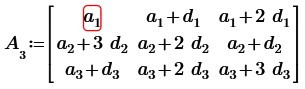
В первой и третьей строке  возрастающая арифметическая погрессия, а во второй строке убывающая арифметическая прогрессия.

По свойству матриц транспонируем данную матрицу:

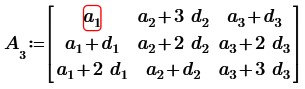
Вычтем из второй и третьей строки первую строку, получим:

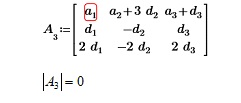
Как мы видим, вторая строка пропорциональна третьей строке с коэффициентом пропорциональности, равным 2. А, значит, определитель данной матрицы будет равен 0.

3. В исходной матрице (см. п. 1) заменим элементы любой строки произвольными числами. Выясним, при каких значениях этих чисел определитель полученной матрицы будет равняться нулю.

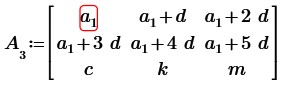
Вычтем из второй строки первую строку, получим:

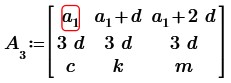
По свойству матриц транспонируем полученную матрицу:

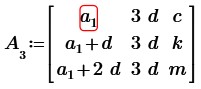
Вычтем из второй и третьей строк первую строку, получим:

Вычислим определитель данной матрицы:

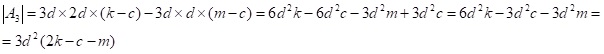
Приравняем определитель матрицы к 0:

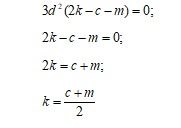
Мы видим, что число k равно полусумме чисел c и m и находится между ними. Это свойство является характерным для последовательных членов арифметической прогрессии.

Т.е. определитель матрицы третьего порядка, составленный из последовательных членов арифметической прогрессии и тремя произвольными числами в одной из строк (столбцов), будет равен нулю тогда и только тогда, когда указанные числа будут являться последовательными членами этой либо другой арифметической прогрессии.

 

 

4.1.2 Исследование вырожденности квадратных матриц четвертого порядка и выше, составленных из последовательных членов одной или разных арифметических прогрессий

 

1. Заполним матрицу четвертого порядка разными арифметическими прогрессиями, т.е. в каждой строке – члены разных арифметических прогрессий:

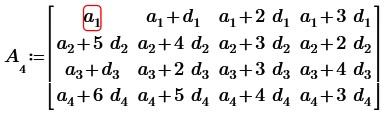
В первой и третьей строках записана возрастающая арифметическая прогрессия, а во второй и четвертой строках - убывающая арифметическая прогрессия.

По свойству матриц транспонируем данную матрицу:

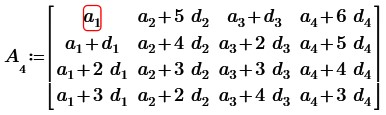
Вычтем из второй, третьей и четвертой строк первую строку, получим:

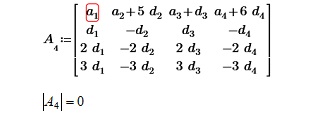
Как мы видим, вторая строка пропорциональна третьей (коэффициент пропорциональности равен 2) и четвертой строке (коэффициент пропорциональности равен 3); также третья строка пропорциональна четвертой строке (коэффициент пропорциональности равен 1,5). А, значит, определитель матрицы будет равен 0.

2. Возьмем квадратную матрицу 4-ого порядка, составленную из последовательных членов одной арифметической прогрессии и заменим произвольную строку (столбец) произвольными числами.

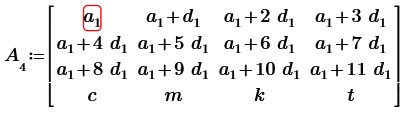
Вычтем из второй и третьей строк первую строку, получим:

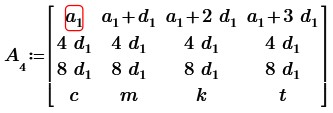
Как мы видим, вторая и третья строки пропорциональны. Вычтем из третьей строки вторую строку, умноженную на 2:

По свойству матриц, если все значения одной из строк (столбцов) равны 0, то определитель этой матрицы будет равен 0.

3. Найдем определитель матрицы четвертого порядка, в которой каждая новая строка (столбец) состоит из последовательных членов новой арифметической прогрессии. Причем, заменим одну из данных строк (или столбцов) произвольными числами.

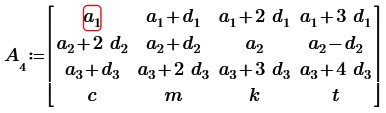
По свойству матриц транспонируем данную матрицу:

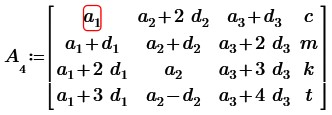
Вычтем из второй, третьей и четвертой строк первую строку получим:

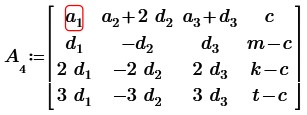
Вычтем из третьей и четвертой строк вторую строку, умноженную на 2 и умноженную на 3 соответственно:

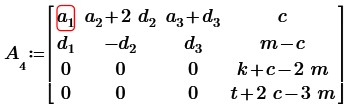
Вычислим определитель данной матрицы, разложением по 4 столбцу:

Как мы знаем, если в матрице одна из строк (или столбцов) состоит из нулей, то определитель этих матриц даст значение нуль. То есть мы получаем:

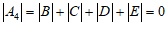
То есть, определитель матрицы 4-ого порядка, состоящей из последовательных членов разных арифметических прогрессий (в каждой строке новая арифметическая прогрессия), причем в одной из строк стоят произвольные числа, все равно даст значение нуль!

В ходе исследования мы сформулировали Гипотезу 2.

Гипотеза 2. Квадратная матрица порядка n≥4, составленная из последовательных членов одной или разных арифметических прогрессий для каждой строки (столбца), при замене (n-3) строк (столбцов) или их сочетаний произвольными числами, будет всегда вырожденной.

4. Вычислим определитель матрицы 10-ого порядка, в которой каждая новая строка (столбец) состоит из последовательных членов другой арифметической прогрессии.

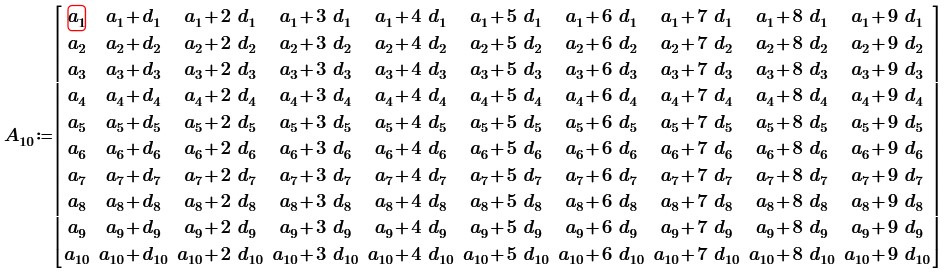
Очевидно, что определитель данной матрицы равен нулю. Покажем это:

Вычтем из 2, 3, 4 … 10 столбца первый столбец, получим:

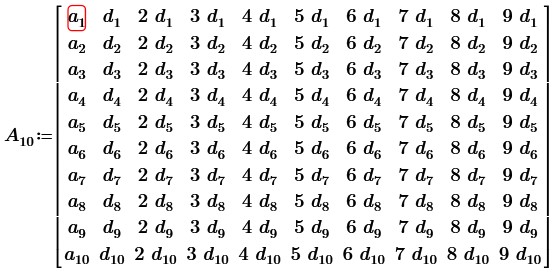
Очевидно, что 2 – 10 столбцы пропорциональны, следовательно, определитель данной матрицы равен нулю.

Проверим гипотезу 2 на квадратной матрице 10-ого порядка, т.е заменим (10-3) строк (столбцов) или их сочетания на произвольные числа: p₁, p_{2, …} p_n

Очевидно, при замене семи любых столбцов среди оставшихся трех столбцов два - будут всегда пропорциональны, следовательно, определитель данной матрицы будет равен нулю.

При замене семи строк произвольными семьюдесятью числами матрица также останется вырожденной:

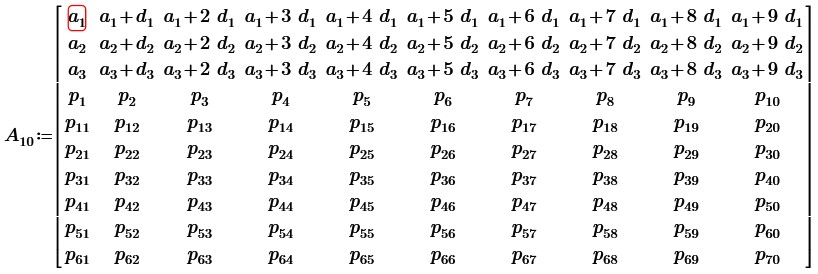
Транспонируем данную матрицу:

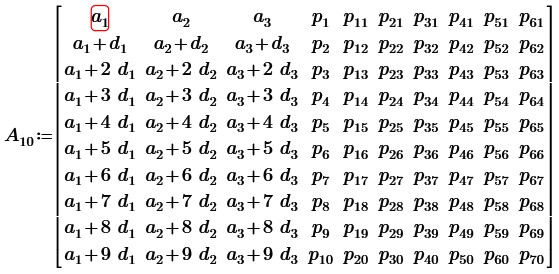
Вычтем из 2, 3 … 10 строк первую строку. Примем p₂-p₁=q₂; p₃-p₁=q₃; … p₁₀-p₁=q₁₀; p₁₂-p₁₁=q₁₂; … p₇₀-p₆₁=q₇₀, получим:

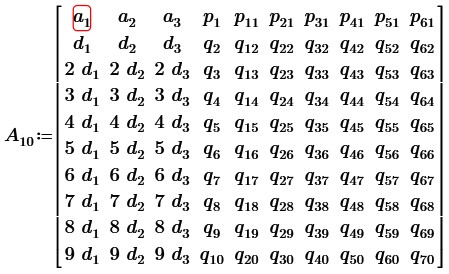
Мы видим, что в первых трех столбцах строки со второй по десятую пропорциональны. Произведем вычитание из 3, 4 … 10 срок вторую строку, умноженную соответственно на 2, 3, 4 … 9. Примем разности в столбцах 4-10 и строках 3-10 соответственно равными: s₃; s₄; … s₇₀. Получим матрицу:

Вычислим определитель данной матрицы, как сумму произведений элементов первого столбца на их алгебраические дополнения.

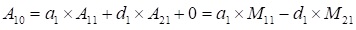
Раскроем эти миноры:

При вычислении определителей M₁₁ и M₂₁ по первому столбцу, как суммы произведений элементов первого столбца на их алгебраические дополнения, получаем значение нуль. Следовательно, 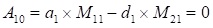 – матрица вырожденная.

Если мы заменим 3 строки и 4 столбца (или их любой комбинации) на произвольные числа, мы получим также вырожденную матрицу. Покажем это:

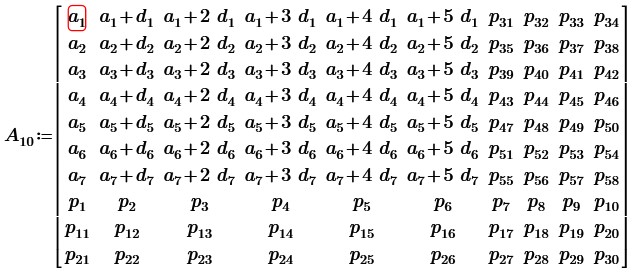
Транспонируем эту матрицу:

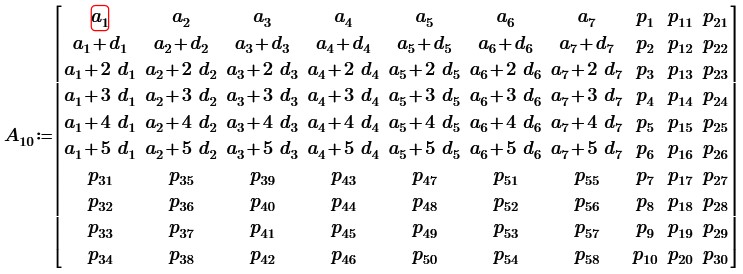
Вычтем из 2, 3 … 6 строк первую строку. Примем p₂-p₁=q₂; p₃-p₁=q₃; … p₆-p₁=q₆; p₁₂-p₁₁=q₁₂; … p₂₆-p₂₁=q₂₆, получим:

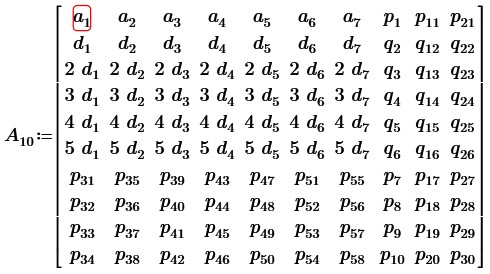
Видим, что строки 2-6 пропорциональны в первых семи столбцах. Вычтем из 3-6 строк вторую строку, умноженную на соответствующие коэффициенты. Примем разности в столбцах 8-10 в строках 3-6 соответственно равными: s₃; s₄; … s₂₆. Получим матрицу:

Вычислим определитель этой матрицы через сумму произведений элементов десятого столбца на их алгебраические дополнения:

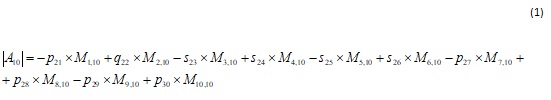
Полученные миноры являются определителями девятого порядка. Каждый определитель девятого порядка вычислим, как сумму произведений элементов 9 столбца на их алгебраические дополнения. Таким образом получили сумму определителей 8-ого порядка, умноженные на соответствующие коэффициент.

Вычислим каждый минор 8-ого порядка, как сумму произведений элементов 8 столбца на их алгебраические дополнения. Получим сумму определителей 7-ого порядка, умноженные на соответствующие коэффициент. Причем значение каждого определителя 7-го порядка равно нулю. Объясним это.

За трёхэтапное вычисление определителя исходной матрицы A₁₀ мы получили сумму произведений определителей 7-ого порядка на соответствующие коэффициенты. Каждый полученный определитель 7-го порядка состоит из элементов семи строк и семи первых столбцов.

В вычисляемой матрице (1) присутствует 4 нулевые строки по седьмой столбец.  Для вычисления определителей 7-ого порядка, мы берем первые семь столбцов и семь любых строк. Любые семь строк данной матрицы всегда содержит как минимум одну нулевую строку. Поэтому все определители 7-го порядка равны 0.  Следовательно, определитель матрицы 10 порядка равен нулю.

Гипотеза 2 о вырожденности квадратной матрицы 10-го порядка при замене 7 строк (столбцов) или их сочетаний на произвольные числа, верно!

5. Докажем, что квадратная матрица n-ого порядка, в которой каждая новая строка (столбец) состоит из последовательных членов другой арифметической прогрессии, сохраняет свойство вырожденности при замене (n-3) строк (столбцов) или их сочетаний на произвольные числа: p∈{p_n(n-3)}

Пусть дана квадратная матрица n-ого порядка, каждый столбец которой состоит из последовательных членов другой арифметической прогрессии.

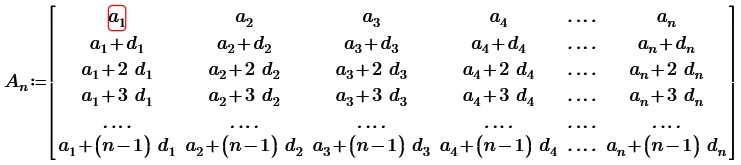
Вычтем из 2, 3, … n строк первую строку, получим:

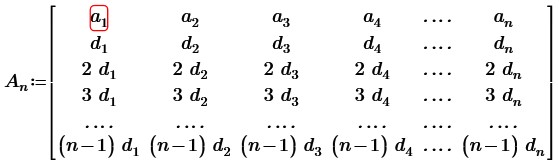
Очевидно, что 2, 3 … n строки пропорциональны, следовательно, определитель данной матрицы равен нулю, т.е. матрица вырожденная.

Таким образом гипотеза 1 о вырожденности квадратной матрицы, заполненной последовательными членами одной или разных арифметических прогрессий для каждой строки (столбца) – Доказана.  

В исходной матрице A_n заменим x cтолбцов на произвольные числа, где n≥x+3. Тогда мы можем изменить только (n-3-x) строк. (Мы можем изменить любые строки и столбцы, но для удобства доказательства мы меняем последние строки и столбцы). Неизменными останутся (n-x) столбцов и (x+3) строк.

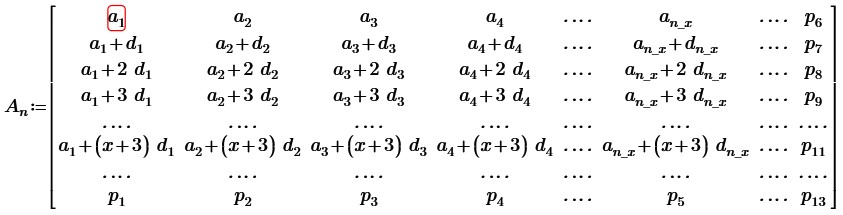
Вычтем из 2, 3, … ,(x+3) строк первую строку. Обозначим разности, получающиеся в x последних столбцах через букву q, где q∈{q_x(x+2)}.

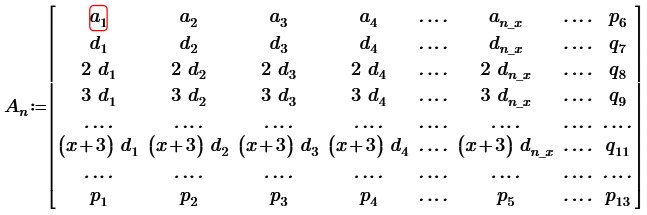
Мы видим пропорциональность строк со 2-ой по (x+3) в первых (n-x) столбцах.

Вычтем из 3-ей, 4-ой, … ,(x+3) строк первую строку умноженную на соответствующие коэффициенты. Разности в последних x столбцах обозначим буквой s, где s∈{s_x(x+1)}.

Мы получили в первых (x+3) строках и первых (n-x) столбцах только две ненулевые строки, а остальные (x+1) – нулевые строки.

Вычислим определитель матрицы через суммы произведений элементов n-ого столбца на их алгебраические дополнения. Эти алгебраические дополнения являются определителями (n-1) порядка. Дальнейшее вычисления сводим к понижению порядка миноров в алгебраических дополнениях до столбца (n-x).

Все миноры порядка (n-x) содержат как минимум одну нулевую строку. Докажем это:

В результате преобразований ушло x последних столбцов, и x строк. Выше мы доказали, что количество нулевых строк в матрице A_n равно (x+1). Следовательно, в минорах как минимум остается одна нулевая строка.

Следовательно, каждый минор равен нулю. И определитель матрицы A_n равен нулю.

Т.е. матрица n-ого порядка, строки (столбцы) которой состоят из последовательных членов разных арифметических прогрессий, при замене (n-3) строк (столбцов) или их сочетаний на произвольные числа, остается вырожденной. Иными словами, гипотеза 2 доказана.

 

Нами был сделан следующий важный вывод.

При исследовании квадратных матриц любого порядка, начиная с 3-го, наблюдаются закономерности:

I) квадратная матрица, составленная из последовательных членов арифметической прогрессии, начиная с любого номера, является вырожденной;

II) квадратная матрица, составленная из последовательных членов разных арифметических прогрессий для каждой строки (столбца), является вырожденной.

III)  квадратная матрица порядка n≥4, составленная из последовательных членов одной или разных арифметических прогрессий для каждой строки (столбца), при замене (n-3) строк (столбцов) или их сочетаний произвольными числами, будет всегда вырожденной.

 

Научная новизна работы заключается в том, что в ней сформулированы и подробно обоснованы новые свойства отрезков прогрессирующих последовательностей (и некоторых других) длиной, равной квадрату натурального числа (начиная с 3:  3² = 9): равенство нулю определителя, элементы которого составлены из последовательных членов арифметических прогрессий.

Наиболее существенный результат исследования, обладающий научной новизной – вывод о том, что квадратные матрицы порядка больше трёх, составленные из последовательных членов арифметический прогрессий (для каждой строки, столбца), обладают помехоустойчивостью. Иначе говоря, замена в таких матрицах какой-либо строки или столбца на совершенно произвольные числа, не влияет на значение ее определителя – он равен нулю.

Авторы продолжают исследования условия вырожденности квадратных матриц, составленных из элементов других последовательностей.

1. Селеменев,  В.Ф.  Научно-исследовательская  работа  студентов: доступность, качество, востребованность / В.Ф. Селеменев, Ю.П. Афиногенов // Вестник Воронежского государственного университета. - № 1, 2008. – С. 37-41.
2. Лазарев, В.С. Критерии и уровни готовности будущего педагога к исследовательской деятельности / В.С. Лазарев, Н.Н. Ставринова // Педагогика. – № 2, 2006. – С.51-59.
3. Беллман Р. Введение в теорию матриц. Изд-во: Мир. – 1990. – с. 368.
4. Курош А.Г. Курс высшей алгебры. Учебник для университетов. – Изд-во Наука. Глав.ред. физ.-мат. литературы. Москва. – 1968. – с. 431
5. Смольняков И.М., Часов К.В. Некоторые свойства прогрессирующих последовательностей // Международный журнал экспериментального образования. – 2014. – № 7 ч.1. – С. 106-107.
6. Смольняков И.М., Часов К.В. Исследование различных последовательностей // Материалы VI Международной студенческой электронной научной конференции «Студенческий научный форум» URL: www.scienceforum.ru/2014/729/6698 (дата обращения: 12.12.2018).
7. Черепов К.Р., Часов К.В. Подготовка интерактивного обучающего документа по изучению свойств арифметических прогрессий // Прикладные вопросы точных наук / Материалы III Международной научно-практической конференции студентов, аспирантов, преподавателей, посвящённой 60-летию со дня образования Армавирского механико-технологического института. 2019. С. 331-334.