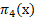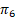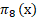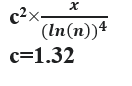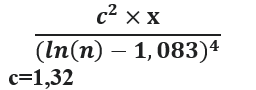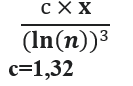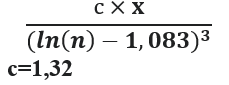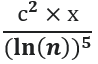Исследование близнецов и структур близнецов простых чисел в интервалах до 1000000000

Простые числа известны и исследовались с глубокой древности, но до сих пор хранят в себе много тайн. Проблемы, связанные с простыми числами, которые не решены математиками до сих пор, хорошо известны и о них можно прочитать вследующей литературесм.: [1], [2], [3],[4], [5].В данной с работе исследовались близнецы простых чисел, то есть простые числа, отличающиеся на 2 и структуры , состоящие из рядом стоящих близнецов. Числа находились в интернет ресурсах, в основном это -https://calculat.io/ Список  простых чисел. Следует отметить, что структуры из рядом стоящих близнецов простых чисел, а именно структуры вида: Блз.-n-Блз, где n – составное число, практически не исследовались.

Как известно формулу для нахождения числа простых чисел в заданном интервале предложил еще Гаусс :

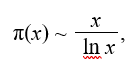
где функция π(x) – это зависимость числа простых чисел с возрастанием натуральных чисел,  и хотя в дальнейшем данная формула усовершенствовалась, известна формула, которую дал Лежандр:

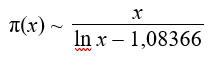
на достаточно больших интервалах формула Гаусса хорошо работает (см. таблицу 1). В работах [4] и [6] исследовались близнецы простых чисел и число близнецов в заданном интервале. Автор [4] предложил формулу для нахождения числа близнецов в заданном интервале:π₂(х)=C×х/ln² x, где  C – постоянная, приблизительно равная 1,32 (точнее C = 1,3203236316...).Функция  π₂(x) –зависимость числа близнецов простых чисел с возрастанием простых чисел.Даннуюформулу  автор вывел, опираясь на теорию вероятности. Как видно из таблицы №1, которую представил автор [4], вышеприведенные формулы хорошо согласуютсяc фактическими результатами.

Таблица 1

Простые числа и простые-близнецы в 8 интервалах длины 150 000.  (взята из [4])

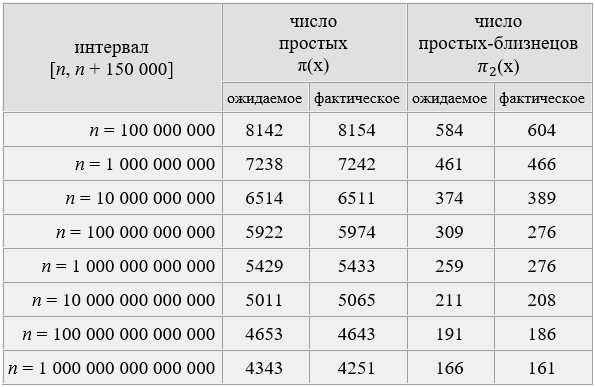
Как известно [8] все пары чисел-близнецов, кроме (3, 5), имеют вид:  6n±1 (n – натуральное) или,  если учитывать также делимость на 5, то окажется, что все пары близнецов, кроме первых двух имеют вид : 30n±1 или 30n+12±1 или 30n+18±1, перебирая все случаи с приведенными формулами, в данном случае мы имеем 14 вариантов ,а именно размещения 4 по 2, 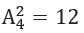 +2варианта с одинаковыми формулами, ( вычитая 2 число из 3го и учитывая, что чисел между близнецами на 1 меньше) мы можем получить nтолько кратное 3, а именно: n=3;9;15;21;27;33;39;45;51 и так далее.что нашло подтверждение в данном исследовании.Были  просмотрены интервалы: [0 - 100000] ;[299000-303000] ; [900000-1000000] и [999900000-1000000000]. Результаты приведены в Приложении.

На практике были найдены  следующие структуры Блз.-3-Блз. (квадруплеты) -35 в интервале: [0-100000]; 4 в интервале: [299000-303000]; в интервале: [900000-1000000]; и 2 в интервале: [999900000-1000000000] . Блз.-9-Блз. :50 в интервале: [0-100000]; 13 в интервале:[900000-1000000]   и 2 в интервале: [999900000-1000000000] . Блз.-15-Блз. , 14 в интервале: [0-100000], 1 в интервале: [299000- 303000]; 8 в интервале: [900000-1000000] и 1 в интервале: [999900000-1000000000]. Блз.-21-Блз. , 9 в интервале: [0- 100000] и 2 винтервале:[900000-1000000]. Блз.-27-Блз. , 9 в интервале: [0-100000];3 в интервале: [900000-1000000] и 4 в интервале: [999900000-1000000000].Блз.-33-Блз., 2 в интервале : [0-100000] и 4 интервале : [900000-1000000] .Блз.-39-Блз.:3 в интервале [900000-1000000] и  1 в интервале:[999900000-1000000000]. Блз.-51-Блз. , 1 в интервале: [0-100000]. Блз.-57-Блз.,  1 в интервале: [999900000-1000000000].Блз-63-Блз : 1 в интервале: [900000-1000000].  Все результаты представлены в Приложении. Как видно изприведенных результатов все квадруплеты: (Блз.-3-Блз.) имеют одну и тужеструктуру, а именно : первое число заканчивается 1, второе 3, третье 7, четвертое 9.Это также подтверждает литература см. например [7].

Кроме того в интервале [0-100000] есть структуры из 3 близнецов подряд:

Блз.-n-Блз.-m-Блз. из 4 близнецов подряд: Блз.-9-Блз.-3-Блз-21-Блз., а в интервале [900000-1000000] мы нашли структуру из 5 близнецов подряд: Блз.-9-Блз.-15-Блз.-9-Блз.-9-Блз.  Эта структура по-видимому вообще является уникальной , по крайней мере в диапазоне до 1000000.  Все они представлены в Приложении.

Как уже указывалось ранее число простых чисел пропорционально   1/lnх , число близнецов пропорционально   1/ln² x , естественно предположить ,опираясь на известную из теории вероятности формулу для независимых событий: P(A∩B) = P(A)·P(B)  ,  что  структуры, которые содержат 2 близнеца подряд Блз.-n-Блз., (их число в интервале) будет пропорционально:

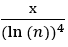
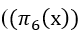 ,а не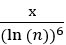

Для структур вида: Блз.-n-Блз.-m-Блз.-k-Блз.  (четыре близнеца подряд)  формула имела вид, пропорциональный: 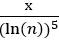, а не .

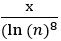Тот факт, что число структур виду: Блз.-n-Блз. пропорционально 1/(ln(n))³ , а не 1/(ln(n))⁴  , а число структур вида: Блз.-n-Блз.-m-Блз. пропорционально 1/(ln(n))⁴ , а не  1/(ln(n))⁶ , говорит о том, что близнецы в этих структурах (их появление друг за другом) не является абсолютно независимым.  

 Результаты вычислений представлены в таблице №2.

Таблица №2

Анализируя, результаты представленные в таблице , можно сделать вывод, что исследованные  нами структуры: Блз.-n-Блз. имеют одно значение вероятности, причем все структуры Блз.-n-Блз. надо считать в сумме, не зависимо от значений n , то есть именно сумма всех структур вида:  Блз.-n-Блз. ,наиболее подходит под следующие формулы: 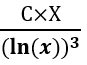  и 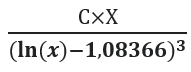 , где с=1,32.

Из этого следует, что общее число структур вида: Блз.-n-Блз.  (сумма Блз.-n-Блз. для различных n )в каком либо достаточно большом интервале наиболее стабильная величина, причем,  чем дальше интервал расположен,  тем в этом интервале будут  преобладать структуры вида: Блз.-n-Блз. с более большими значениями n, так в интервале [0- 100000] преобладают структуры :Блз.-3-Блз. и Блз.-9-Блз., а в интервале: [999900000-1000000000] преобладают структуры вида: Блз.-27-Блз.

Тот факт, что число структур виду: Блз.-n-Блз. пропорционально 1/(ln(n))³ , а не 1/(ln(n))⁴  , а число структур вида: Блз.-n-Блз.-m-Блз. пропорционально 1/(ln(n))⁴ , а не  1/(ln(n))⁶ , говорит о том, что близнецы в этих структурах (их появление друг за другом) не является абсолютно независимым.  

Как известно  до сих пор не решена проблема близнецов, нет   доказательства: бесконечен ли ряд близнецов или он конечен, хотя абсолютное число математиков считает, что этот ряд бесконечен. Действительно сейчас известны близнецы:   2996863034895×2^1290000±1 [7], это число с 388348 десятичных знаков. Возникает закономерный вопрос: может ли ряд чисел вида:  Блз.-n-Блз. тоже быть бесконечным или он конечен? Возможно да, может. По крайней мере удалось найти  структуру вида: Блз.-27-Блз., о области чисел 2100000000 вот она:  (2100007961;2100007963;2100007991;2100007993)

Выводы:

1. Исследованы новые структуры внутри ряда простых чисел. Структуры вида: Блз.-n-Блз. и  Блз.-n-Блз.-m-Блз. Найдены структуры из 4, рядом стоящих близнецов Блз.-n-Блз.-m-Блз.-k-Блз.  и структура из 5, рядом стоящих близнецов :(909287;909289;909299;909301;909317;9093019;909329;909331;909341;909343)
2. Предложены формулы для нахождения числа структур Блз.-n-Блз. и Блз.-n-Блз.-m-Блз. в заданном интервале.
3. 5. Найдена структура вида Блз.-27-Блз. , в области чисел 2100000000 :  (2100007961;2100007963;2100007991;2100007993).
4. Ряд простых чисел содержит в себе множество различных структур, присутствие которых и определенная последовательность их появления, показывает внутреннюю структурированность всего бесконечного ряда простых чисел.

ПРИЛОЖЕНИЕ:

Интервал: [0-100000]

Интервал: [290000-303000]

Интервал: [900000-1000000]

Интервал: [999900000-1000000000]

Списки,  шести, восьми и десяти, рядом стоящих простых чисел,  состоящие из 3, 4 и 5 близнецов:

                Интервал [0-100000]

1. Вид шестерки: Блз.-9-Блз.-3-Блз., :(809;811;821;823;827;829)
2. Вид шестерки:Блз.-9-Блз.-15-Блз., : (3359;3361;3371;3373;3389;3391)
3. Вид шестерки:Блз.-9-Блз.-9-Блз. :(4217;4219;4229;4231;4241;4243)
4. Шестерка:Блз.-15-Блз.-9-Блз., :(6761;6763;6779;6781;6791;67930)
5. Восьмерка: Блз.-9-Блз.-3-Блз.-21-Блз.,:(9419;9421;9431;9433;9437;9439;9461;9463)
6. Шестерка: Блз.-3-Блз.-9-Блз. , :(18041;18043;18047;18049;18059;18061)
7. Шестерка: Блз.-9-Блз.-9-Блз.,:(21587;21589;21599;21601;21611;21613)
8. Шестерка: Блз.-15-Блз.-9-Блз.,:(26861;26863:26879;26881;26891;26893)
9. Шестерка: Блз.-21-Блз.-3-Блз.,:(67187;67189;67211;67213;67217;67219)
10. Шестерка:Блз.-21-Блз.-15-Блз., : (80447;80449;80471;80473;80489;80491)
11. Шестерка: Блз.-9-Блз.-9-Блз.,:(91127;91129;91139;91141;91151;91153)
12. Шестерка: Блз.-3-Блз.-9-Блз.,:(97841;97843;97847;97849;97859;97861)      

Интервал [900000-1000000]

1. Шестерка: Блз.-21-Блз.-3-Блз.

(907367;907369;907391;907393;907397;907399)

2. Десятка: Блз.-9-Блз.-15-Блз.-9-Блз.-9-Блз.

(909287;909289;909299;909301;909317;9093019;909329;909331;909341;909343)

3. Шестерка: Блз.-9-Блз.-9-Блз., :

(983429;983431;983441;983443;983447;983449)

1. habr.com Простые числа: история и факты / Хабр  Перевод оригинала: J.J.O^ࢭConnorandE.F.Robertson
2. postnauka.ruПростые числа.  Джеймс Мэйнард
3. Грасиан Энрике « Простые числа. Долгая дорога к бесконечности»
4. Дон Цагир  «Первые 50 миллионов простых чисел»
5. Integral-russia.ruМагия простых чисел: примеры и неожиданные открытия.
6. file:///C:/Users/seste/Downloads/o-raspredelenii-prostyh-chisel-i-prostyh-chisel-bliznetsov-v-naturalnom-ryade-do.pdf. О распределении простых чисел и простых чисел-близнецов в натуральном ряде до x = 400000000. Андрухаев Х.М.
7. Числа-близнецы — Википедия (wikipedia.org)