Инженерные расчеты: основа эффективного проектирования роботов

В рамках участия в проекте «Энергия в каждой капле» группа обучающихся по ДОП «Образовательная робототехника» посещали Верхотурскую ГЭС. В ходе экскурсии ребята узнали о проблеме обеспечения безопасности пешеходов на лестничных пролетах в связи с образованием снега и льда на ступенях, что увеличивает риск травматизма работников ГЭС.

Было решено разработать и создать макет робота, способного передвигаться по перилам лестниц и выполнять очистку ступеней от снега и льда.

Для создания макета был использован конструктор LEGO. Это решение позволило реализовать функциональную модель с минимальными затратами времени и ресурсов, сохранив при этом возможность адаптации конструкции к различным условиям эксплуатации. Представленная модель робота может быть применима как в жилых домах, так и в общественных зданиях и различных производствах, где требуется регулярная очистка лестниц в зимний период.

Перед созданием макета обучающимися по программе «Решение технических задач» был произведен предварительный расчет некоторых параметров модели.

Для конструирования робота рассчитаем радиус колес, которые необходимо взять для модели и устойчивость конструкции к перевороту назад. Известно, что:

Угол наклона перил: 25⁰

Материал перил: полипропиленовая труба.

Коэффициент трения между перилами и колесами: по таблице от 0,01 до 0,03

Система сцепления: две пары колес из конструктора LEGO. Колеса обеспечивают надежное сцепление с перилами, что является ключевым фактором для работы робота в условиях наклонной поверхности.

Цели исследования:

1. Определить условия предотвращения соскальзывания робота при движении его вверх.

2. Найти параметры, при которых робот не опрокинется назад.

Для определения условий, при которых робот не будет соскальзывать с перил, рассмотрим силы, действующие на колеса робота.

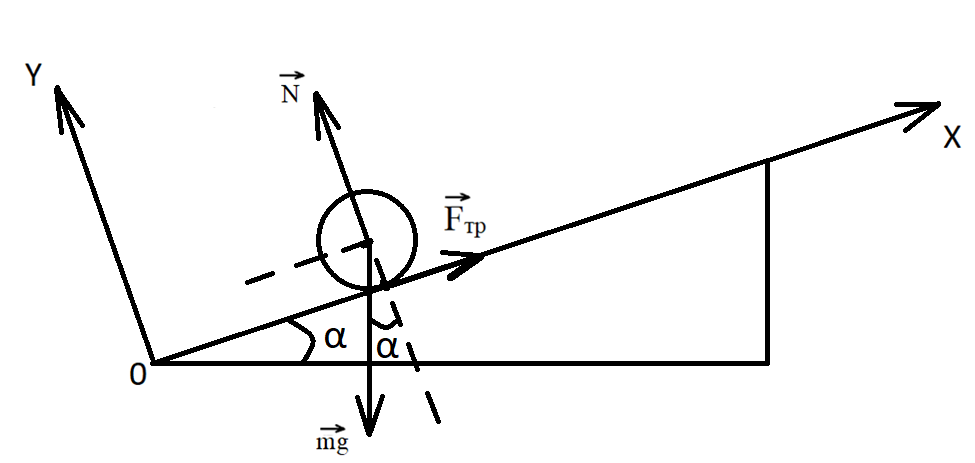
Рисунок 1. Силы, действующие на колеса робота

Изобразим на рисунке все силы, действующие на колесо робота: силу тяжести, силу реакции опоры и силы трения качения.

Из рисунка 1 видно, что колесу мешает соскальзывать сила трения качения, легко предположить, что есть некоторое пограничное значение силы трения, при котором колесо не будет двигаться вниз.

Найдем от чего зависит сила трения. Для этого решим классическую задачу динамики.

Запишем второй закон Ньютона в векторном виде:

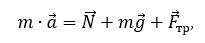
 где mg - сила тяжести, N – сила реакции опоры, F_тр – сила трения качения.

Спроецируем данное уравнение на оси координат:

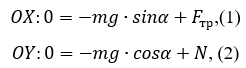
Запишем формулу силы трения качения

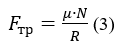
где R – радиус колеса, μ – коэффициент трения скольжения колеса.

Выразим из (2) N и подставим в (3)

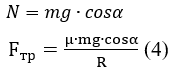
Подставим (4) в (1)

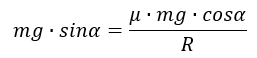
Сокращая на mg, получим:

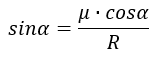
Тогда 

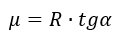
В итоге получили минимальный коэффициент трения колес, при котором робот не будет соскальзывать вниз. Выразим радиус колеса, при котором это возможно:

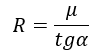
Далее определяется условие, при котором робот при движении не опрокидывается назад.

Для упрощения расчета примем, что материал робота однородный. Опрокидывание робота происходит при условии, если линия действия силы тяжести выходит за пределы площади опоры робота.

Рассмотрим пограничное условие, когда линия действия силы тяжести проходит через крайнюю точку опоры (Рис. 2). Установим связь между высотой и длиной робота при заданном угле, исходя из рисунка.

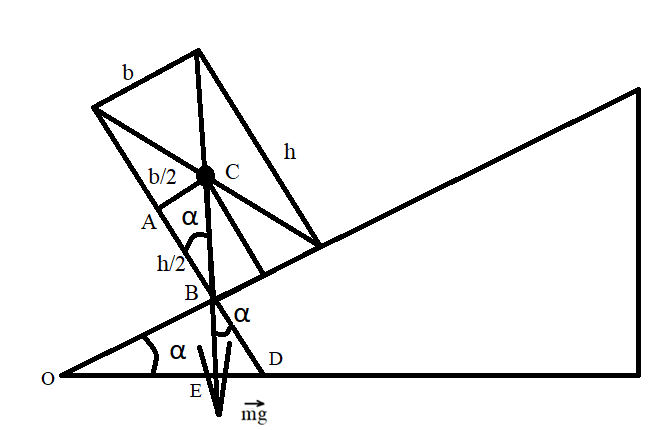
Рисунок 2. Линия действия силы тяжести проходит через крайнюю точку опоры

На рисунке треугольники OBD и BED прямоугольные и имеют общий угол D, равный 90 – α. Тогда угол EBD равен α. Углы EBD и ABC вертикальные, значит они равны по свойству вертикальных углов. Треугольник ABC также прямоугольный, поэтому для него справедливо соотношение

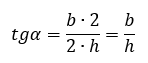
Отсюда

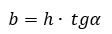
Робот будет устойчив на наклонной поверхности при условии

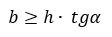
Рассмотрим основные параметры и характеристики разработанного устройства:

Масса: 1900 граммов. Масса робота была выбрана таким образом, чтобы устройство обладало достаточной устойчивостью на перилах и могло преодолевать сопротивление трения, не теряя сцепления с поверхностью.

Ширина: 43 см. Длина конструкции обеспечивает равномерное распределение массы и устойчивость при движении по наклонной поверхности.

Длина: 15 см. Узкий профиль робота позволяет ему перемещаться по стандартным перилам, сохраняя баланс и маневренность.

Высота: 15 см. Компактная высота снижает вероятность переворачивания робота и облегчает его транспортировку.

Вычислим размеры колеса робота, при которых робот не будет соскальзывать:

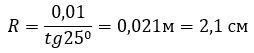
Для конструирования робота использовали с запасом колеса радиусом 3,5 см.

Проверим на устойчивость собранного робота

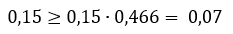
Условие устойчивости выполняется, и робот не переворачивается.

Выводы:

1. Для предотвращения проскальзывания колёс при заданном коэффициенте трения необходимо использовать колеса большего диаметра.
2. Для предотвращения опрокидывания требуется снижение высоты центра тяжести за счет установки тяжелых элементов конструкции в нижней передней части робота или увеличение длины и уменьшение ее высоты базы робота, что также приводит с снижению высоты центра масс.

Предварительные теоретические расчеты играют ключевую роль в процессе проектирования робота. Они позволяют:

• Определить параметры основных конструкций.

Теоретические расчеты позволяют точно понять требования к размерам, массе и другим характеристикам робота. Это помогает избежать ошибок, таких как недостаточное сцепление колес или неустойчивость конструкции, которые могут сделать робот непригодным для выполнения задачи.

• Минимизировать риск неудачи.

Расчеты позволяют заранее оценить поведение робота в различных условиях эксплуатации. Например, расчет коэффициента трения и устойчивости гарантирует, что робот сможет передвигаться по перилам без риска проскальзывания или опрокидывания.

• Снизить затраты на материалы и обучение

Теория позволяет сократить количество экспериментов. На основании расчетов выбираются оптимальные параметры конструкции, позволяющие сократить затраты на материалы и временные затраты на сборку и обучение.

• Учет условий эксплуатации

Физические расчеты учитывают такие факторы, как угол наклона поверхности, коэффициенты трения, силу тяжести и т.д., что делает проектирование более точным и адаптированным к реальным условиям.

• Повышенная безопасность

Гарантия устойчивости и предотвращения проскальзывания в критических ситуациях для предотвращения аварийных ситуаций во время эксплуатации.

На основании этого можно сделать вывод, что предварительные теоретические расчеты предназначены для создания эффективного и безопасного прототипа робота. Они обеспечивают научно обоснованный подход к проектированию, повышению надежности и функциональности конечного устройства. Углубленное изучение физических процессов помогает учащимся развивать инженерное мышление. Это дает возможность не только решать конкретные задачи, но и понимать, как различные физические законы действуют в той или иной ситуации. Такой подход способствует формированию у будущих инженеров способностей анализировать, прогнозировать и принимать обоснованные проектные решения.

1. Проектирование машин, роботов и мехатронных систем. Сборник материалов Всероссийской научно-методической конференции - Орел: ОГУ имени И.С.Тургенева, 2017. - 76 с.
2. В. Г. Хомченко Робототехнические системы: Учебное пособие Омск 2016 г. – 195 стр.
3. Геометрия. 7 – 9 классы: учеб. для общеобразоват. организаций / [Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев и др.]. – 2-е изд. – М.: Просвещение, 2014. – 383 с.
4. Заяц А. В., Путилова А. А., Гуляева Л. И. Профориентация в инженерном образовании: опыт работы технопарка «Кванториум» МАОУ Политехническая гимназия // Научные высказывания. 2024. №20 (67). С. 33-36.