Использование циклов и условий при решении многоуровневых геометрических задач с использованием Dobot Magician
Рассмотрены основные понятия математики, необходимые для написания программы. Приведена примерная программа разбиения окружности на равные части с использованием циклов и условий на разных уровнях сложности. Даны рекомендации по написанию программы.
Одним из модулей при реализации ДОП «Прикладная робототехника» является решение геометрических задач различного вида, причем одно и тоже задание может быть решено на разных уровнях сложности.
Задания первого уровня рассчитаны на учащихся, не имеющих подготовки в области геометрии и программирования.
В основном эти задачи решаются нерационально при помощи простых манипуляций. Программирование сводится к реализации линейного алгоритма, а программа содержит набор простых действий и перемещений. Решение задач на данном уровне позволяет учащимся поверить в свои силы. Как правило, программы, реализующие алгоритмы по решению геометрических задач, получаются громоздкие, и учащиеся уже в процессе написания испытывают желание их упростить или оптимизировать, что подталкивает их к изучению нового материала.
Задания второго уровня ориентированы на учащихся имеющих подготовку по геометрии и программированию и позволяют научиться применять знания для решения практических задач. Такие задачи обычно решаются при помощи простых программ с использованием нелинейного алгоритма, содержащего обычно 1 цикл или условие.
Задачи третьего уровня рассчитаны на учащихся продвинутого уровня подготовки, желающих совершенствовать свои знания в программировании.
На данном уровне учащимся предоставляется или совершенно новая неизвестная задача, решение которой он должен найти в различных источниках информации, а преподаватель направляет и корректирует действия, или осуществляется модернизация готовой программы по заданным преподавателем условиям.
Рассмотрим пример реализации задачи о разбиении окружности заданного радиуса на заданное количество равных частей на разных уровнях.
При выполнении на первом уровне учащиеся, в основном, строят циркулем окружность заданного радиуса, затем делят на нужное количество равных частей при помощи транспортира и определяют (измеряют или вычисляют) координаты точек относительно центра окружности.
Для учащихся второго уровня перед выполнением задачи необходимо разобрать некоторые понятия из геометрии, которые они на момент написания программы или не проходили, или проходили частично в школьном курсе математики.
Для начала совместно с учениками решается математическая задача, суть которой состоит в том, чтобы разбить окружность на заданное количество одинаковых частей и определить координату каждой точки.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси. Для Dobot Magician, если смотреть сверху, оси расположены следующим образом: OX – вверх, OY – влево.
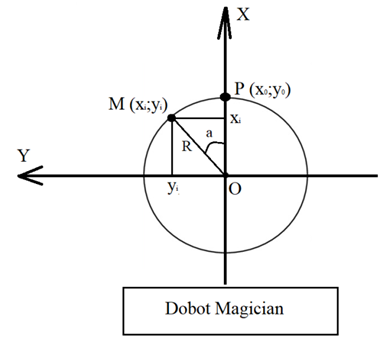
Рисунок1. Окружность на координатной плоскости Dobot Magician
В программе точка Р имеет начальные координаты x0 = 250 мм; y0 = 0 мм. Чтобы посчитать координаты точки М, воспользуемся формулами:
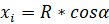
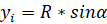
Чтобы посчитать, чему равен угол а, нужно задать количество частей, на которое надо поделить окружность. В общем виде, обозначим это количество за n. Тогда угол а найдем по формуле:
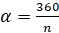(т.к. вся окружность составляет 3600)
Переходим к составлению программы. Сама программа написана в Scratch, выполняется при помощи вакуумного захвата (присоски). На начальных этапах присоска проще, чем пневматический захват. В точки на окружности, образующиеся после разбиения, для наглядности устанавливаются кубики. Данная программа была подробно описана в источнике [4], поэтому здесь возьмем лишь ее краткое описание.
1. Выбрать вакуумный захват с помощью команды.
2. Установить высоту прыжка при режиме движения Jump (П-образная траектория).
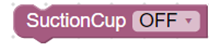
3. Выбрать режим работы вакуумного захвата с выключенным насосом.
4. Задать начальные данные, присвоив переменным начальные значения.
5. Задать цикл по переменной z.
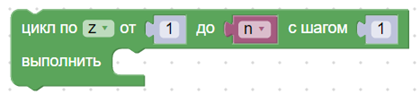
6. Задать формулу для угла поворота.
7. Задать формулу для координат точки при угле поворота а.
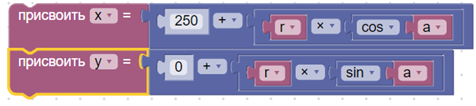
8. Переместить захват в начальную точку, куда будут устанавливаться кубики вручную.
9. Включить захват и захватить кубик.
10. Переместить кубик в точку с расчетными координатами.
11. Выключить захват и отпустить кубик.
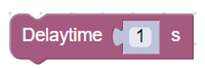
12. Во время выполнения всех операций рекомендуется между командами цикла устанавливать задержку по времени 1 – 2 с, чтобы было удобно подставлять кубики в начальную точку.
13. Поднять стрелу робота и закончить работу.
Для учащихся третьего уровня в данной задаче были сделаны следующие усложнения:
- Присоску заменили на пневматический захват, поэтому приходится учитывать габариты лапок клешни и пневмоцилиндра, а также угол поворота, при котором можно брать и ставить кубики.
- Кубики на начальной позиции устанавливаются в виде ряда, а не подставляются учащимся в одно и тоже место, где робот их берет.
- Кубики при постановке должны быть ориентированы вдоль окружности, т.е. угол поворота кубика перед постановкой постоянно меняется.
- Все используемые величины свести к нескольким изначально задаваемым переменным, сделав программу более универсальной
Как определить координаты точек, куда нужно поставить кубики, описано выше для второго уровня.
На третьем уровне необходимо определить, на какой угол нужно поворачивать кубик на каждом шаге. Для этого построим окружность произвольного радиуса и укажем на ней 2 положения кубика (рис.2)
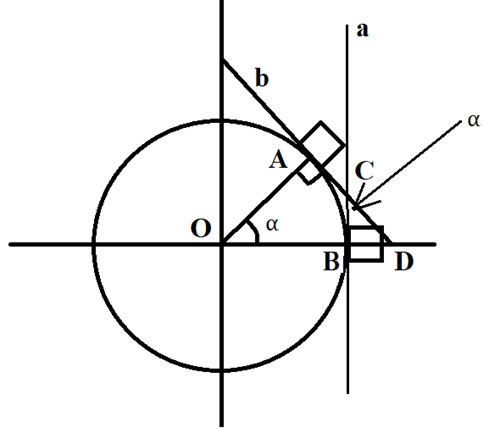
Рисунок 2. Решение задачи с поворотом кубиков
Отрезки ОА и ОВ являются радиусами окружности. Проведем касательные a и b к окружности в точках А и В. При этом видно, что касательная совпадает со стороной кубика, которую нужно повернуть на определенный угол, такой же, как и угол, на который поворачивается касательная.
Получилось 2 прямоугольных треугольника OAD и BCD с общим углом D. Эти треугольники подобны по первому признаку подобия треугольников. При этом угол С будет равен углу О, а угол С – угол, на который нужно повернуть касательную, т.е. искомый.
Переходим к составлению программы. Данная программа написана также в Scratch.
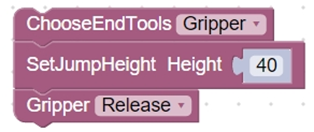
- Выбираем пневматический захват, устанавливаем высоту прыжка и переводим захват в открытое положение.
- Присваиваем значения переменных: n – количество частей, на которые нужно разбить окружность, z – переменная, от которой зависит номер шага в цикле, r – радиус окружности, xнач и yнач – начальные координаты точки, где находится первый кубик.
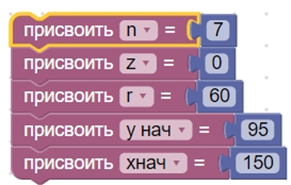
- Задаем цикл по переменной z.
- Задаем формулу для угла поворота.
- Задаем формулу для координат точки при угле поворота а.
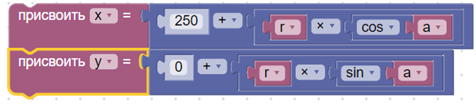
- Далее робот должен взять кубик из точки с координатами (xнач; yнач; -30), повернув клешню на 900. При выполнении данной операции возникли сложности с тем, что:
- если команду SetR, осуществляющую поворот, поставить до команды Jump, то робот сначала поворачивает насадку, но при дальнейшем перемещении поворачивает ее назад;
- если команду SetR поставить после команды Jump, то робот сначала опустит насадку, а уже потом на месте будет ее поворачивать, но при этом соседние кубики в ряду мешают взять кубик.
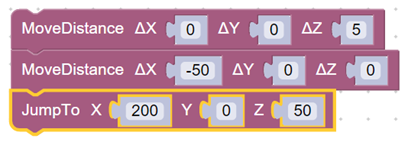
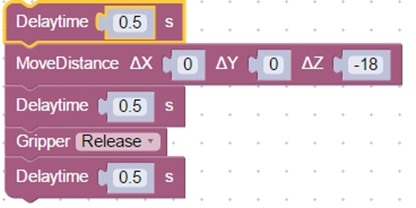
Поэтому предлагается один из выходов из данной проблемы: сначала перемещаем насадку в точку выше той, где находится кубик, поворачиваем насадку и опускаем ее при помощи команды MoveDistance.
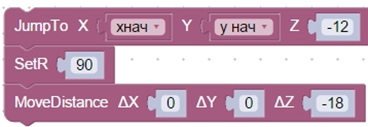
- Далее координата Х каждого последующего кубика увеличивается на длину ребра кубика, т.е. на 20 мм.
- При закрывании захвата желательно прописать время задержки при закрытии захвата. В противном случае робот будет совершать 2 одновременных движения: закрывать лапки и двигаться вверх к конечной точке команды Jump. В этом случае робот возьмет кубик не за центральную часть, а за самый верх, и точность по координате Z нарушится.
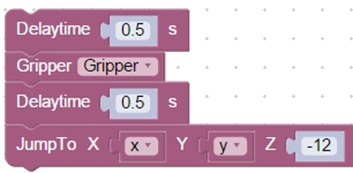
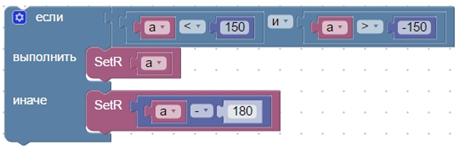
- При установке кубика с поворотом на определенный угол возникло следующее обстоятельство: насадка может поворачиваться не на 3600, а в диапазоне от -1500 до 1500. Для решения проблемы использовали блок условия. Если угол принадлежит указанному диапазону, то кубик поворачивается на это угол, в противном случае, робот поворачивает насадку на угол α – 180.
- Робот опускает насадку и раскрывает ее, освобождая кубик.
В результате проделанной работы учащиеся получают навыки по математике и программированию, анализу незнакомых данных для решения поставленной задачи, решению практических задач в реальных условиях, когда исходные данные могут изменяться, а условия выполнения программы становится более сложными.
- Программирование манипулятора в срeде COOGLE BROCKLY: DOBOT MAGICIAN: Образовательная инженерная платформа/ О.А. Горнов. – М.: Издательство «Экзамен», 2021. – 188[1] с.
- Dobot Magician. Руководство пользователя. — М.: ИНТ, 2018. — 114 с.
- Геометрия. 7 – 9 классы: учеб. для общеобразоват. организаций / [Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев и др.]. – 2-е изд. – М.: Просвещение, 2014. – 383 с.
- Заяц А. В., Зубиков А. А. Использование Dobot Magician для формирования инженерного мышления у учащихся 7-8 классов // Научные высказывания. 2023. №10 (34). С. 40-43.
