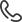Использование Dobot Magician для формирования инженерного мышления у учащихся 7-8 классов

Одной из дополнительных образовательных программ технической направленности, реализуемой в детском технопарке «Кванториум», является «Прикладная робототехника». Обучающиеся по данной программе осваивают навыки работы на роботизированном манипуляторе Dobot Magician, учатся управлять производственными объектами. Работа на манипуляторе способствует расширению знаний по математике и информатике, а так же  формированию инженерного мышления.

Одна из задач, над которой учащиеся работают в процессе обучения  по программе, – разбиение окружности заданного радиуса на заданное количество равных частей. В ходе реализации программы манипулятор разбивает окружность заданного радиуса на заданное количество частей. В местах разбиения окружности манипулятор выставляет объект, например, кубик.

Для написания программы разбиения окружности необходимо сначала разобрать с учениками среднего звена некоторые понятия из геометрии, которые они на момент написания программы или не проходили, или проходили частично.

Для создания модели и описания программы понадобятся следующие понятия из математики:

1. Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве.

2. Прямоугольная система координат – это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

3. Координатные оси – это прямые, образующие систему координат.

4. Ось абсцисс OX – горизонтальная ось на плоскости.

5. Ось ординат OY – вертикальная ось на плоскости.

6. Координатная плоскость – плоскость, в которой находится система координат. Обозначается так: XOY.

7. Ось аппликат OZ – вертикальная ось перпендикулярная координатной плоскости.

8. Единичный отрезок – величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

9. Окружность – это множество всех точек на плоскости, находящихся на одинаковом расстоянии от данной точки.

10. Радиус окружности – отрезок, соединяющий любую её точку с центром. Все радиусы окружности равны.

11. Градус – это 1/360 часть окружности.

12. Градусная мера угла – это положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле.

13. Единичная окружность – это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.

14. Прямоугольный треугольник – треугольник, у которого один угол – прямой, т.е. равный 90°. Сторона прямоугольного треугольника, лежащая напротив прямого угла, называется гипотенузой, а две другие стороны – катетами.

Рис.1 Прямоугольный треугольник: a и b – катеты, c – гипотенуза.

15. Теорема Пифагора: квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин его катетов.

a²+b²=c²

16. Синус угла – отношение противолежащего катета к гипотенузе.

17. Косинус угла – отношение прилежащего катета к гипотенузе.

После рассмотрения и освоения основных математических понятий учащимися необходимо провести контрольный срез знаний по степени усвоения учениками данного материала. Приступать к дальнейшему решению задачи следует с теми учениками, которые освоили материал.

Для начала с учениками решается математическая задача, суть которой состоит в том, чтобы разбить окружность на заданное количество одинаковых частей и определить координату каждой точки.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси. Для Dobot Magician, если смотреть сверху, оси расположены следующим образом: OX – вверх, OY – влево.

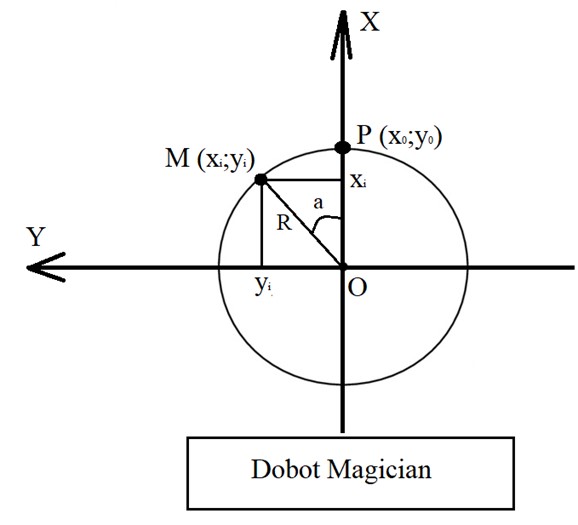
Рис.2 Окружность на координатной плоскости Dobot Magician

В программе точка Р имеет начальные координаты x₀ = 250 мм; y₀ = 0 мм. Чтобы посчитать координаты точки М, воспользуемся формулами:

xi=R*cosa

yi=R*sina

Чтобы посчитать, чему равен угол а, нужно задать количество частей, на которое надо поделить окружность. В общем виде, обозначим это количество за n. Тогда угол а найдем по формуле:

a=360:n (т.к. вся окружность составляет 360⁰)

Переходим к составлению программы. Сама программа написана в Scratch, выполняется при помощи вакуумного захвата (присоски). В точки на окружности, образующиеся после разбиения, для наглядности устанавливаются кубики.

Далее следует поэтапный разбор каждой команды с пояснениями.

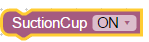
• Выбрать вакуумный захват с помощью команды

• Установить высоту прыжка при режиме движения Jump (П-образная траектория)

Высоту прыжка выбираем 30 мм, исходя из следующих соображений. Во-первых, высота кубика – 20 мм, и при перемещении кубики будут цепляться друг за друга, по этой же причине не допускается перемещение кубика по прямой. Во-вторых, устанавливать высоту больше, нельзя при радиусах, близким к предельным: робот сможет дотянуться по прямой, но при подъеме выйдет за пределы рабочей зоны и выпадет в ошибку.

• Выбрать режим работы вакуумного захвата с выключенным насосом

На начальном этапе насос выключен для сокращения времени его работы, экономии электроэнергии и снижения уровня шума.

• Задать начальные данные, присвоив переменным начальные значения

Переменная n – количество частей, на которое нужно разбить окружность, z – номер шага, r – радиус окружности в мм. Радиус в 74 мм оказался предельным, поэтому его значение должно быть меньше 74 мм.

• Задать цикл по переменной z

Значение z меняется либо от 1 до n, либо от 0 до n – 1. Выбирать значение от 0 до n нельзя, т.к. совершив полный оборот, робот попытается поставить n-й кубик на место нулевого, упрется в стол. При этом может сбиться нулевое положение робота и придется его перезагружать.

• Задать формулу для угла поворота

Начальный угол задаем равным нулю, и с каждым шагом добавляется угол, рассчитанный по формуле: a=360:n.

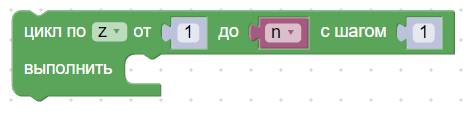
• Задать формулу для координат точки при угле поворота а

Координаты начальной точки Р (250;0). Координаты последующих точек рассчитываются по формулам геометрии через sina и cosa.

• Переместить захват в начальную точку, куда будут устанавливаться кубики вручную.

Здесь точку можно взять любую в пределах рабочей зоны.

• Включить захват и захватить кубик.

• Переместить кубик в точку с расчетными координатами

Координата z меняться не будет, т.к. высота кубиков одинаковая.

• Выключить захват и отпустить кубик.

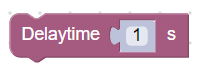
• Во время выполнения всех операций рекомендуется между командами цикла устанавливать задержку по времени 1 – 2 с, чтобы было удобно подставлять кубики в начальную точку.

• Поднять стрелу робота и закончить работу.

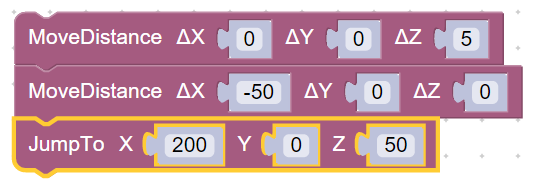
Данные команды опциональные. Подъем стрелы робота может быть достигнут разными путями. В данном случае сначала приподнимаем захват на 5 мм. Затем смещаем по оси Х ближе к роботу на 50 мм, а затем выводим робота в произвольную точку. Подъем стрелы при помощи движения типа  JUMP из данного положения невозможен из-за выхода насадки за пределы рабочей зоны робота.

1. Программирование манипулятора в срeде COOGLE BROCKLY: DOBOT MAGICIAN: Образовательная инженерная платформа/ О.А. Горнов. – М.: Издательство «Экзамен», 2021. – 188[1] с.
2. Dobot Magician. Руководство пользователя. — М.: ИНТ, 2018. — 114 с.
3. Геометрия. 7 – 9 классы: учеб. для общеобразоват. организаций / [Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев и др.]. – 2-е изд. – М.: Просвещение, 2014. – 383 с.