Эвристические задачи как средство формирования математических умений школьников

Изучение математики играет системообразующую роль в образовании, развивая познавательные способности человека, в том числе к логическому мышлению, влияя на преподавание других дисциплин. В последние десятилетия резко выросло значение математических методов в социально-экономических, биомедицинских науках и языкознании. Качественное математическое образование имеет фундаментальное значение в современном обществе, построенном на информационных технологиях. Ряд нормативных документов на уровне Правительства Российской Федерации ставят задачу «повышения качества преподавания математики и естественно-научных предметов в государственных и муниципальных общеобразовательных организациях».

Обучающийся в свою очередь должен не просто освоить базовый курс математики. Целью обучения математике наряду с овладениями конкретными математическими знаниями, необходимыми для применения в практической деятельности, является интеллектуальное развитие обучающихся, формирование качеств мышления, а также приобретение универсальных (общих) способностей, умений и навыков, являющихся основой существования человека в социуме.

Передаточный характер овладения изучаемым материалом неэффективен для полноценного формирования умений.  Сегодня учитель должен обеспечить обучающихся необходимым набором методов и средств, при помощи которых школьники смогут самостоятельно продолжать познавательную деятельность, обучаться и развиваться. Таким образом, современный учитель предстаёт не как источник информации, но как носитель методов обучения и опыта.

Педагоги сходятся во мнении, что управлять процессом усвоения математических умений, корректировать их, а также поощрять и стимулировать приобретение новых моделей умений позволяет процесс решения задач. Однако, при существующем многообразии типовых математических задач педагоги недооценивают возможности поисковых, эвристических задач, рассматривая их как средство работы с более одаренными школьниками.

На данный момент существует небольшое количество научной и методической литературы, где давались бы методические рекомендации по использованию на уроках задач, способствующих самостоятельному открытию математических фактов. Невелика и численность таких задач в рекомендуемых учебниках. Это вызывает трудности для включения их в методику преподавания математики.

В психолого-методической литературе сложилось единое представление о понятии «умение». В самом общем виде оно формулируется как «элемент деятельности, позволяющий что-либо делать с высоким качеством, точно и правильно выполнять какое-либо действие, операцию, серию действий или операций» [9, с.158-159]. Процесс образования умений происходит в результате объединения системы знаний, координации действий и их регуляции. Изменчивость и возможность приспособления действий к изменяющимся время от времени условиям деятельности, возможность изменения структуры умений и последовательность их выполнения, сохраняя при этом неизменным конечный позитивный результат работы – это то, что отличает умения от заученных или бессознательно выполняющихся действий.

Изучением умений как результатов математической деятельности занимались такие исследователи, как Н.Д. Стефанова, Н.С. Подходова, которые в свою очередь различали интеллектуальные и аналитические умения школьников. Интеллектуальные умения включают в себя анализ, синтез, сравнение, обобщение, специализацию, абстрагирование, конкретизацию, классификацию и систематизацию. Дополняя этот список, Л.Н. Косякова выделяет ещё «умение последовательно и логично выстраивать сложные концепции, делать верные логические выводы, умение планировать наперёд, умение удерживать в голове несколько последовательных шагов» [6, с.5-6].

Аналитические умения – это умения, главным образом связанные с выполнением операции сравнения, выделением главного, выявлением закономерностей, абстрагированием, конкретизацией и систематизацией. Таким образом, аналитические умения используются при осуществлении широкого круга действий, так как составляющая этих умений – установление причинно-следственных связей. Помимо яркой аналогии с доказательством теоремы, аналитические умения, например, необходимы при сложении и вычитании рациональных дробей, решении уравнений и неравенств и т.д. [12, с.146-151].

Рассматривая развитость мышления и приобретение умений как единый процесс, авторы приходят к выводу, что развитие данных умений происходит преимущественно при решении задач, которые позволяют управлять процессом усвоения умений, корректировать их, а также поощрять и стимулировать приобретение новых моделей умений. При этом сами задачи становятся одновременно объединяющим элементом и отдельным умением, сочетающим в себе ряд других умений.

В самом общем виде понятие задачи формулирует Г.А. Балл «это система, обязательными компонентами которой являются: а) предмет задачи в его исходном состоянии; б) образ требуемого состояния предмета задачи» [1, с.203]. Приведённая выше формулировка удобна тем, что в ней содержатся обязательные компоненты задачи и она чётко указывает специфику систем, представляющих собой задачи.

Под эвристической задачей понимается задача, в которой известен только один её компонент – условие, и неизвестны теоретический базис решения, способ решения и искомое. Это означает, что обучающемуся следует в результате самостоятельного поиска теоретического базиса, определить предмет искомого, найти способ решения и решить задачу. При этом результатом решения задачи будут выступать не только ответ на поставленный в задаче вопрос, но и приобретённые эмпирическим путём знания. По мнению А.Г. Иодко, эвристические задачи – это предъявляемые обучающимся задания, содержащие проблему, решение которых требует проведение теоретического анализа, применение одного или нескольких методов научного исследования, с помощью которых обучающиеся сами откроют ранее неизвестные для них знания [10, с.102-104]. Такого вида задачи ещё называют проблемными, но это синонимичные определения.

Эвристическими задачами могут стать «задачи на применение уже известных закономерностей в относительно новых условиях, но таких, которые предполагают перестройку знакомых способов решения, выбор наиболее рационального способа действия, применение общих теоретических положений, принципов решений в реальных практических условиях, требующих внесения в них конструктивных изменений» [14, с.412-414].

Целостная эвристическая задача требует от обучающихся различных умений, среди которых анализировать условие задачи, разбивать задачу на подчинённые ей, уметь выделять главное и осуществлять поиск информации, составлять план решения задачи, и качеств, таких как гибкость ума, потребность отыскивать причины явлений, высказывание своего мнения, желание и готовность к активной учебной деятельности, умение организовать себя и свою работу, навык рефлексии, интуитивное мышление [11, с.227]. Система специально разработанных эвристических задач помогает школьнику овладеть умением самостоятельно выполнять каждый из этапов решения, открывая для себя новые математические факты.

Значение эвристики в школе на уроках математики трудно переоценить. Эвристические задачи выполняют многие дидактические функции: систематизация учебного материала; формирование умения «добывать знания»; способ, приводящий к математическому открытию; умение разбивать условие задачи на составляющие; способствуют познавательной активности; развивают творческие способности; вырабатывают исследовательские навыки.

Ю.Н. Кулюткин предлагает вводить эвристические задачи на уроках математики, основываясь на фазе развития ситуации решения эвристических задач, тем самым подчёркивая динамику развития математических умений [7, с.173-183].

Первая фаза – ситуация ориентировки ребёнка. На данном этапе обучающимся предлагаются эвристические задачи с большой степенью определенности содержания. При решении подобных задач обучающиеся выносят первичные представления о связи математики как науки и учебного предмета с материальным миром, о значимости действенных знаний и умений. Причем эти представления достаточно прочные, так как добыты в результате деятельности, то есть с трудом. На этом этапе происходит развитие познавательного интереса и познавательной потребности, формируются умения анализировать, сравнивать и обобщать, видеть понятия, понимать их значение в условии задачи, связывать действиями при решении.

Вторая фаза - ситуация поиска. Основанием для создания ситуаций служат эвристические задачи, требующие творческой переработки содержания. В ходе этого дальнейшее развитие получают способности обучающихся к рефлексии. Кроме того, формируется умение ставить вопросы, отвечая на которые учащиеся достигают осознания средств и оснований собственной деятельности, проявляется способность отказаться от навязчивой идеи, преодолеть инерцию мышления перехода к новому методу решения. Здесь важно общение ребят друг с другом, так как именно через других человек становится собой. В ходе диалога «ученик - ученик» каждый ученик может апробировать собственный путь решения задачи с риском неудачи или негативной оценки результата. Здесь формируются умение отстаивать собственное мнение, иметь независимость суждений и готовность отказываться от неверного пути в случае обнаружения ошибки.

Третья фаза – ситуация преобразований, основанием для создания которых служат эвристические задачи оптимальной неопределенности содержания. Целью данного этапа является осознание и переживание ребенком ценности и смысла познания, когда интерес вызывает не результат, а сам процесс решения эвристической задачи, процесс познавания. Вся работа по решению эвристических задач осуществляется в процессе свободного общения, обмена мнениями, в творческой дискуссии. Определяющим условием при этом является личная включенность учащегося в процесс. Подобная организация учебного процесса оказывает существенное влияние на развитие у ребят способности к поиску альтернатив, открытости, восприимчивости к анализу и критике, умений генерировать идеи, выдвигать гипотезы, прогнозировать решения творческой задачи, видеть противоречия и на основе анализа проблемных ситуаций формулировать проблемы [13, с.18].

Четвертая фаза - ситуация интеграции. Деятельность ученика в этой ситуации характеризуется проявлением субъективного, мировоззренческого отношения к изученным фактам и способам их объяснения, самостоятельным нахождением проблем, парадоксов и противоречий, проявлением эвристической позиции в учебном процессе. При таком виде деятельности происходит интеграция ранее полученных знаний и умений с теми, которые отрабатываются в текущий момент, также происходит автоповторение необходимых знаний, ранее заученных тем, их трансформация и реконструирование с учетом специфики творческой задачи. На этой ступени обучающимся предлагаются эвристические задачи, охватывающие несколько тем курса [13, с.18].

Методика эвристического обучения математике строится на основе традиционной системы обучения путём её расширения и усовершенствования и включает в себя набор эвристических методов и приёмов. При этом эта методика необходима как одарённым детям, так и отстающим ученикам, потому как изучение самой математики происходит с опорой на их личностные особенности. Создавая свои образовательные продукты, являющиеся непосредственно фактами в математике, обучающиеся переходят по ступеням сложности, достигая тех же результатов, что и обучающиеся с ярко выраженной хорошей обучаемостью.

Наиболее полно эвристические приёмы представлены у Е.И. Скафа, которые она подразделяет на общие и специальные. К общим автор относит анализ через синтез, сравнение, абстрагирование, обобщение, классификация, систематизация и т.д. Приведём назначения и правила использования некоторых из них. Применение анализа через синтез осуществляется этапами: расчленить на части анализируемые объекты и рассмотреть переход одного из них в новую систему связей и отношений, установив при этом новые свойства исходного объекта, соотнести полученные свойства объекта с поиском первоначального результата. Данные операции полезны при обучении школьников решениям задач на доказательство. Сравнение – это средство связи новых и ранее усвоенных знаний, учебного материала и личного опыта обучающихся. При сравнении свойств объектов следует выделять не только общие из них, но и отличные. Овладение приёмом сравнения способствует, например, предотвращению ошибок по аналогии и выдвижению правдоподобных гипотез по аналогии. Абстрагирование даёт возможность вычленить существенные свойства, связи и отношения, лежащие в основе существования явления или объекта. Правилом абстрагирования является выделение свойств объекта, от которых нужно отвлечься, и найти их в других предметах. Обобщение – приём, применение которого предполагает выявление существенного общего свойства из множества объектов. Классификацию следует применять так, что сначала изучается объект, затем вспоминается родовое понятие, к которому относиться данный объект, и все существенные свойства родового понятия будут соотносится с такими же свойствами изученного объекта.

В специальных Е.И. Скафа выделяет эвристический довод, т.е. правдоподобная гипотеза, эвристические рассуждения, основанные на индукции и аналогии, эвристические стратегии, те общие рекомендации по решению эвристических задач, и эвристические схемы.

Другую классификацию эвристических приёмов можно найти у          Ю.Н. Кулюткина. Он сопоставляет их со звеньями эвристического поиска: упрощение задачи с сохранением её элементов; проведение аналогии элементов задачи; нахождение вспомогательных отношений через продуцирование инвариантов и их вычленения; пересечение. Первые два приёма осуществляются с использованием метода движения от конца к началу и наоборот, приёмов доказательства от обратного. Третий приём основывается на дополнительных преобразованиях объектов задачи. И, наконец, вся задача решается путём движения к общему и от него – к частному [7, с.35].

Имея ввиду указанные выше методические приёмы решения задач, способствующих самостоятельному открытию математических фактов, и классификации Б.А. Кордемского [3, с.234-236], Л.М. Фридмана [15, с.187], опишем общие эвристические приёмы (Таблица 1).

Таблица 1

Эвристические приёмы решения задач

Рассмотрим решение задач, способствующих самостоятельному открытию математических фактов, с использованием эвристических приёмов.

Задача 1.

Найдите корни уравнения 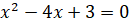 [4, с.174].

Для решения этого задания школьникам, не изучавшим алгоритм решения уравнений данного вида, необходимо вспомнить формулы сокращённого умножения и правила решения уравнения вида x-ax-b=0, где a и b какие-то числа, а x – неизвестная переменная. Затем, имея ввиду формулы сокращённого умножения, разложить исходное уравнение на две скобки и, приравнивая каждую из них к нулю, найти корни уравнения. При этом, следует отметить, что решить задачу школьники смогут, применяя эвристические приёмы: анализ, разбиение целого на части, переход к равносильной задаче, метод исследования. В этом случае исходная задача является для школьников эвристической.

Задача 2.

Решите пример 2⁴∗4³. Как можно упростить решение задачи? Получится ли верное значение, если число 2 возвести в 10 степень, а число 4 в 5 степень? Для каких чисел можно применять этот метод? [8, с.25].

Для того, чтобы решить эту задачу школьникам нужно будет вспомнить лишь понятие степени и применить эвристические приёмы, такие как аналогия, обобщение, метод конструирования правил, метод дополнительных преобразований. В результате чего обучающиеся овладеют материалом по теме: «Свойства степени».

Задача 3.

Нарисуйте прямоугольник с произвольными сторонами. Проведите прямую, соответствующую диагонали прямоугольника. Какие фигуры при этом образовались и будут ли они равны? Вспомните формулу площади прямоугольника и выведите и обоснуйте формулу площади прямоугольного треугольника, получившегося путём предыдущих преобразований прямоугольника [2, с.252].

Решение этой задачи будет означать знакомство с прямоугольным треугольником, его свойствами и нахождением площади прямоугольного треугольника. При этом, учителю следует добиться конкретной формулы площади треугольника с последовательным доказательством её нахождения. Эвристическими методами, способствующими решению этой задачи, будут метод конструирования понятий и правил, метод эвристического наблюдения, метод анализа через синтез.

Приведённые эвристические задачи свидетельствуют о широком круге их применения для формирования у обучающихся понятий, выведению формул и доказательству теорем, успешному усвоению свойств и признаков. Эвристические приемы позволяют решать задачи, не обладая нужными теоретическими знаниями, а сами задачи, в свою очередь, способствуют более глубокому и осознанному изучению учебного материала, расширяют творческо-поисковый потенциал обучаемого, дают возможность систематизировать и интегрировать полученные знания.

Особенностью эвристического обучения математике является предоставление школьникам возможности творить знания, создавать образовательную продукцию по математике в виде умения строить понятия и применять их, высказывать суждения и строить умозаключения, решать разнообразного вида математические задачи, а также способствовать процессу изменения их личностных качеств [11, с.78]. Другими словами, к задаче учителя относится не только преподнесение обучающимся системы математических фактов, но и организация самостоятельного поиска новых закономерностей, развития математической интуиции, знакомства с эвристическими приёмами.

Е.И. Скафа предлагает делить эвристическое обучение на четыре этапа.

1. Конструирование целей обучения. На этом этапе важным является дополнение к учебным умениям эвристических, которые закладывают основу к овладению основными эвристическими приёмами решения задач. Для закрепления и отработки полученных знаний необходимо создавать эвристически ориентированные системы задач.

2. Погружение в эвристическую деятельность. Данный этап предполагает создание учителем эвристических ситуаций, в условиях которых для обучающихся создаются возможности и перспективы открытия знаний и математических фактов. Такое направление внимания школьников позволяет им привыкнуть к ситуации неопределённости в способе решения поставленной задачи и проявить свои эвристические позиции.

3. Решение эвристических задач. Здесь происходит отработка и самостоятельное применение эвристических приёмов в процессе решения задач, способствующих самостоятельному открытию математических фактов. Наработанный опыт решения лёгких эвристических задач ускорит процесс решения трудных.

4. Рефлексивно-оценочная деятельность. При решении эвристических задач важно, чтобы способ решения был найден самими обучающимися. Однако при определённых затруднениях можно предложить подсказки. В рефлексивно-оценочной деятельности полезно разобрать решение задач, которые вызвали затруднения и предложить вопросы, более глубже раскрывающие условия самой задачи [11, с.79-102].

Такой комплексный подход при правильной организации учебного процесса соответствует основной цели эвристического обучения математике-созданию учащимися личного опыта в изучении предмета и получения основного продукта деятельности в виде самостоятельно полученных новых знаний.

Учёт представленных выше ограничений предполагает следование существующим принципам эвристического обучения, которые определяют основные направления работы учителя:

1. Принцип личностного целеполагания ученика: образование каждого ученика происходит на основе и с учетом его личных учебных целей. Осознание целей обучения учеником и учителем обеспечивает продуктивную образовательную деятельность школьников, определяет характер и содержание их дальнейших действий. Из выше сказанного следует, педагогическим требованием к деятельности учителя является привития ученикам навыков целеполагания в обучении.
2. Принцип выбора индивидуальной образовательной траектории: ученик имеет право на осознанный и согласованный с педагогом выбор основных компонентов своего образования. Это значит, что учителя предоставляет обучающемуся свободу в формах и способах выполнения работы, собственном мнении на проблему, индивидуальном поиске её решения.
3. Принцип продуктивности обучения: главным ориентиром обучения является личностное образовательное приращение ученика, складывающееся из его внутренних и внешних образовательных продуктов учебной деятельности. Эвристическое обучение направлено на создание учениками образовательных продуктов, через которое происходит развитие математических навыков и способностей детей.
4. Принцип ситуативности обучения: образовательный процесс строится на ситуациях, предполагающих самоопределение учеников и эвристический поиск их решения. Учитель сопровождает ученика в его образовательном движении, заинтересовывая эвристическими ситуациями и проблемами в них.
5. Принцип образовательной рефлексии: образовательный процесс сопровождается его рефлексивным осознанием субъектами образования. Ученик должен осознать способы деятельности, чтобы запомнить их применение в схожей ситуации [5, с. 121-132].

Таким образом, опыт творческой деятельности в математике невозможен без эвристического обучения школьников. Эвристические приёмы позволяют решать задачи, не обладая нужными теоретическими знаниями, а решение эвристических задач, в свою очередь, влияет на формирование математических умений, способствуют более глубокому изучению учебного материала, расширяют творческо-поисковый потенциал обучаемого, дают возможность систематизировать и интегрировать полученные знания, самостоятельно делать открытия, заполняя пробелы в знаниях. Подход такого обучения строится главным образом на понимании учебных целей всеми участниками образовательного процесса. Задача учителя в данной ситуации совпадает с задачей эвристической деятельности: организация выбора для обучающихся индивидуальной образовательной траектории, которая неразрывно связана с собственным открытием учениками знаний в математике.

1. Далингер, В. А. Методика развивающего обучения математике / В. А. Далингер, Н. Д. Шатова, Е. А. Кальт, Л. А. Филоненко. – М.: Изд. Юрайт, 2022. – С. 12-26.
2. Кордемский, Б. А. Математическая смекалка. Лучшие логические задачи, головоломки и упражнения / Б. А. Кордемский. – М.: Изд. АСТ, 2021. – С. 17-19.
3. Кордемский, Б. А. Сборник занимательных задач для тренировки самостоятельного мышления или математические завлекалки / Б. А. Кордемский. – М.: Изд. АСТ, 2021. – С.25-32.
4. Король, А. Д. Обучение через открытие: в поисках ученика / А. Д. Король. – М.: Изд. Вышейшая школа, 2019. – С. 13-21.
5. Король, А. Д. Эвристическое обучение на основе вопрошания и молчания ученика: от методологии к практике: монография / А. Д. Король. – М.: Изд. Лань, 2020. – С. 44-59.
6. Косякова, Л. Н. Математика. Векторная алгебра: ученое пособие / Косякова Л.Н. – СПб.: Изд. ФГБОУ ВО СПбГАУ, 2023. – С. 65-68.
7. Кулюткин, Ю.Н. Эвристические методы в структуре решения / Ю.Н. Кулюткин. – М.: Изд. Педагогика, 2020. – С.112-117.
8. Лысенкер, Э. М. Прикладные математические задачи для основной и старшей школы / Э. М. Лысенкер. – М.: Изд. Илекса, 2017. – С. 23-26.
9. Немов, Р.С. Психология: Учеб. для студ. высш. пед. учеб. заведений: В 3 кн. – 4-е изд. – М.: Изд. Гуманит. изд. центр ВЛАДОС, 2023. С. 11-19.
10. Подходова, Н. С. Методика обучения математике: учебник для вузов. Ч. 1 / Н. С. Подходова, В. И. Снегурова. – М.: Изд. Юрайт, 2022. – С. 36-40.
11. Скафа, Е. И. Методика обучения математике: эвристический подход. Общая методика / Е. И. Скафа. – М.: Изд. Директ-Медиа, 2022. – С. 233-241.
12. Стефанова, Н.Л. Методика и технология обучения математике. Курс лекций: пособие для вузов / Н.Л. Стефанова, Н.С. Подходова. – 2-е изд, испр. – М.: Изд. Дрофа, 2018. – С. 316-322.
13. Тамилина, Т.В. Содержание понятия «эвристические способности» в контексте современных научных исследований / Т.В. Тамилина // журнал вестник новгородского государственного университета им. Ярослава Мудрого. 2018. №45. С.16-19.
14. Темербекова, А. А. Методика обучения математике / А. А. Темербекова, И. В. Чугунова, Г. А. Байгонакова. – Сбп.: Изд. Лань, 2017. – С. 91-96.
15. Фридман, Л. М. Теоретические основы методики обучения математике / Л. М. Фридман. – М.: Изд. Едиториал УРСС, 2021. – С. 110-115.