Windows — приложение по теории чисел на языке программирования C++

Теория чисел — очень важный раздел математики. Разделы теории чисел лежат в основе таких областей, как криптография, компьютерная графика, кодирование информации и многие другие. Но при решении задач из теории чисел порой требуется большое количество времени.

Цель работы: автоматизирование решения задач из теории чисел и создание приложения, которое помогает при решении таких задач.

Задачи работы:

• Познакомиться с указанными разделами теории чисел
• Составить алгоритм работы приложения.
• Написать программный код.
• Выполнить тестирование программы и устранить недочёты.

Итак, сначала стоит рассказать о теории, которая использовалась в моём приложении.

Определение 1. [1] Показателем целого числа a по модулю m называется наименьшее положительное целое число n ((a, m) = 1), такое, что

aⁿ ≡ 1 ( mod m ).

Проще говоря, это наименьшая натуральная степень n, в которую нужно возвести число a, чтобы при делении aⁿ на m получался остаток, равный 1.

Показатель определен только для чисел a, взаимно простых с модулем m. При этом, если показатель числа a по модулю m определен, то он является делителем значения функции Эйлера φ(m)[1].

Чтобы показать зависимость показателя n от a и m, его также обозначают δ_m(a), а если m фиксировано, то просто δ(a).

Показатель числа по модулю в частности использовался для нахождения длины периода обыкновенной дроби.

Теорема 1. [1] Длина периода в разложении числа 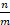 в десятичную дробь равна δ_m(10) (данная теорема работает только для дробей со знаменателями, не кратными 2 и 5).

Доказательство[1].

Рассмотрим дробь

Пусть δ_b(10) = k.

Согласно теореме о делении с остатком, 10a = bc₀ + r₁, где 0 ≤ r₁ < b, (r₁, b) = (10a, b) = 1, так что, в частности, r₁ не может равняться 0, то есть 1 ≤ r₁ < b. Для пары r₁, b мы имеем те же условия что и для a, b, так что мы получаем неограниченную последовательность равенств:

10a = bc₀ + r₁

10r₁ = bc₁ + r₂

 …………

10r_k-1 = bc_k-1 + r_k (1)

где при всех i величины r_i и c_i таковы, что

1 ≤ r_i < b, 0 ≤ c_i = 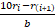 < 10 (r₀ = a) (2)

и при всех i имеем (r_i, b) = 1.

Деля все члены равенств выше соответственно на 10b, 10²b, …, 10^kb, …, получаем  =  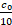+  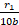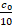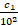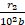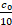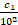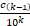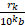=  +  +  = … =  +  + … +  +  = … (3)

Из этого находим

a ∙ 10^k = (c₀ ∙ 10^{k – 1} + c₁ ∙ 10^{k – 2} + … + c_{k – 1}) ∙ b + r_k,

так что r_k ≡ a ∙ 10^k ≡ a (mod b), и поскольку  1 ≤ r_k < b,  1 ≤ a < b, то r_k = a.

Совпадение величин r_k и a показывает, что после k шагов в последовательности равенств выше (1) они начинают периодически повторяться, т. е. c_{k + s}  = c_s при всех s равных 0, 1, 2, …

Поскольку 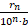 → 0 при увеличении n из равенств (3) получаем периодическое разложение  =  +  + … +  +  +  + … +  + …

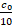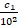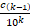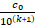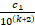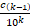Или же сокращённо  = 0, (c₀ c₁ … c_{k – 1}).

Можно утверждать, что найденный период дроби — наименьший.         

Действительно, если  = 0, (c₀ c₁ … c_{k – 1}),

то a ∙ 10^l = (с₀ ∙ 10^{l – 1} + … + с_{l – 1}) ∙ b + a ≡ a (mod b), и поскольку (a, b) = 1,

то 10^l ≡ 1 (mod b),  так что наименьшее значение l = δ_m(10) = k. Теорема доказана.

Для примера определим длину периода дроби .

Как уже ранее говорилось, определения длины периода дроби  необходимо вычислить значение δ₇(10).

φ(7) = 6, значит d | 6 = 1; 2; 3; 6

Начинаем перебор:

10¹ ≡ 3 ( mod 7 )

10² ≡ 2 ( mod 7 )

10³ ≡ -1 ( mod 7 )

10⁶ ≡ 1 ( mod 7 ) -  сравнимо с 1 по модулю 7

Значит, δ₇(10) = 6 ==> длина периода дроби со знаменателем 7 равна 6

Действительно,  = 0,1428571428571… = 0,(142857).

В общем случае, когда знаменатель делится на 2 или 5, ситуация следующая:

Пусть r = 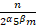; (m, n) = (m, 2) = (m, 5) = 1

Пусть 10^{max{α, β}} = 10^γ

Тогда r ∙ 10^γ = 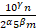 = 2^{γ- α} ∙ 5^{γ- β}  ∙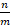

Значит, r =  ∙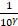

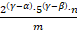
Так как числитель не влияет на длину периода дроби, то длина периода дроби с указанным знаменателем равна δ_m(10), а период будет смещён на γ знаков вправо. В таком случае разложение дроби будет смешанным. [1]

Определение 2. [2] Число a ( (a, m) = 1) называют первообразным корнем по модулю m ( ПК (m) ), если δ_m(a) = φ(m) (φ(m) — функция Эйлера, количество чисел взаимно простых с m и не превосходящих его).

Теорема 2. [1] Первообразные корни существуют только по модулям 2, 4, p, p^α, 2p^α (p > 2).

Пусть g – ПК по модулю m. Тогда для любого целого a ( (a, g) = 1 ) существует такое число γ, что g^γ ≡ a ( mod m ). Тогда число γ называют индексом числа по модулю m (при основании g). [2]

γ = ind_ga

Индекс числа по модулю обладает логарифмическими свойствами, например:

• ind_g(a ∙ b) ≡ ind_g(a) + ind_g(b) ( mod φ(m) )
• ind_g(ab) ≡ ind_g(a) - ind_g(b) ( mod φ(m) )
• ind_g(a^k) ≡ k ∙ ind_g(a) ( mod φ(m) )

Ввиду практической пользы индексов составляются таблицы индексов по определённым К примеру, построим таблицу индексов по модулю 5. В качестве основания возьмём наименьший первообразный корень по модулю 5, то есть 2.

Так как 2 – ПК (5), то 2^φ(5) = 2⁴ ≡ 1 ( mod 5 )

Сначала определим индексы для чисел.

2⁰ ≡ 1(5)

2¹ ≡ 2(5)

2² ≡ 4(5)

2³ ≡ 3(5)

Построим таблицу индексов по данному модулю.

Удобнее построить 2 таблицы: для определения индекса по числу и числа по индексу.

m = 5; φ(m) = 4; g = 2

По модулю вида 2^α таблица индексов строится так:

Если a ≡ (-1)^γ ∙ 5^γ₀ ( mod 2^α ), то система γ, γ₀ называется системой индексов числа a по модулю m (a = 2^α). Причём,

c = 1, c₀ = 1,      если α = 0 или α = 1

c = 2, c₀ = 2^{α – 2}, если α ≥ 2 [2]

К примеру, построим таблицу систем индексов по модулю 8.

Так как 8 = 2³, то c = 2, c₀ = 2.

Построим все возможные сравнения для -1 и 5.

γ = 0 или 1, γ₀ = 0 или 1.

(-1)⁰ ≡ 1 ( mod 8 )

(-1)¹ ≡ -1 ( mod 8 )

5⁰ ≡ 1 ( mod 8 )

5¹ ≡ -3 ( mod 8 )

Попарно перемножим сравнения для (-1) и 5.

(-1)⁰ ∙ 5⁰  ≡ 1 ( mod 8 )

(-1)⁰ ∙ 5¹  ≡ 5 ( mod 8 )

(-1)¹ ∙ 5⁰  ≡ 7 ( mod 8 )

(-1)¹ ∙ 5¹  ≡ 3 ( mod 8 )

И построим таблицу индексов по модулю 8 по полученным данным.

Для произвольного составного модуля систему индексов строят следующим образом:

Пусть m = 2^α ∙ p₁^α₁ ∙ p₂^α₂ ∙ … ∙ p_k^αₖ – каноническое разложение числа m. Пусть g_s – наименьший первообразный корень по модулю p_s^αₛ, s=1, .., k. Если

a ≡ (-1)^γ ∙ 5^γ₀ ( mod 2^α )

a ≡ g₁^γ₁ ( mod p₁^α₁ ), … , a ≡ g_k^γₖ ( mod p₁^α₁ )

то система γ, γ₀, γ₁, … ,  γ_k называется системой индексов числа a по модулю m (всегда (a, m) = 1). [2]

Пример: Построим таблицу систем индексов по модулю 40.

40 = 2³ ∙ 5, следовательно необходимо построить таблицы индексов по модулям 2³ и 5.

Таблицы индексов по модулю 8 и 5 (были построены выше) можно легко продлить до модуля 40, исходя из следующих таблиц:

Из всех таблиц выберем столбцы с общим N и объединим их, тем самым составив таблицу систем индексов по модулю 40.

Заметим, что в таблицах индексов по любому m, все N взаимно просты с m.

Перейдём к самому приложению по теории чисел.

Реализуя поставленную цель, было решено написать приложение, с помощью которого можно переводить обыкновенную дробь в десятичную периодическую, находить длину периода дроби, показатель числа по модулю, значения различных мультипликативных функций, выводить таблицу простых чисел, делители числа, каноническое разложение числа, и с помощью которого можно составлять таблицы индексов по любому числу, не меньшему 2.

Для написания приложения был использован язык программирования C++ из-за быстроты выполнения кода. В моём случае скорость вычислений очень важна. Написание кода происходило в среде разработки Visual Studio. В Visual Studio очень удобно писать код и настраивать проект.

Сначала, уже поставив цель, была начата разработка функций, необходимых для реализации основной цели. Затем, мною разработано всё приложение.

В приложении есть основной класс MNT, внутри которого находятся все необходимые функции, а именно: таблицы простых чисел, делители числа, каноническое разложение числа, вычисления значений различных мультипликативных функций, показатель числа по модулю, деление столбиком, определение длины периода дроби, разложение обыкновенной дроби в десятичную периодическую, нахождение первообразных корней, построение таблиц индексов и систем индексов. Так же есть основная функция main, в которой прописано взаимодействие с пользователем.

Стоит сказать, что построение таблиц индексов и систем индексов работает по тому же алгоритму, приведённому в теоретическом блоке. Перевод обыкновенной дроби в десятичную периодическую работает же по следующему алгоритму:

    1. Из знаменателя дроби m убираются множители 2^α и 5^β.

    2. Вычисляется длина периода дроби по формуле δ_m(10).

    3. Вычисляется γ = max{α, β}.

    4. С помощью деления столбиком вычисляется ( γ + δ_m(10) ) знаков после запятой.

    5. Перед знаком под номером γ + 1 ставим «(»

    6. В конце ставим «)»

    7. Выводим дробь.

При входе в приложение мы видим краткую справку по работе с ним, а именно какому действию соответствует какой номер.

Исходный код приложения расположен в открытом доступе в git репозитории.

Для работы с программой вам необходимо выбрать действие, а затем ввести необходимые данные. После ввода данных действие выполнится автоматически.

Пример 1: переведём дробь  в десятичную периодическую с помощью моей программы. Сначала, выберем номер действия — 12, а затем введём по очереди числитель и знаменатель. Далее сразу выведется разложение данной дроби в десятичную периодическую.

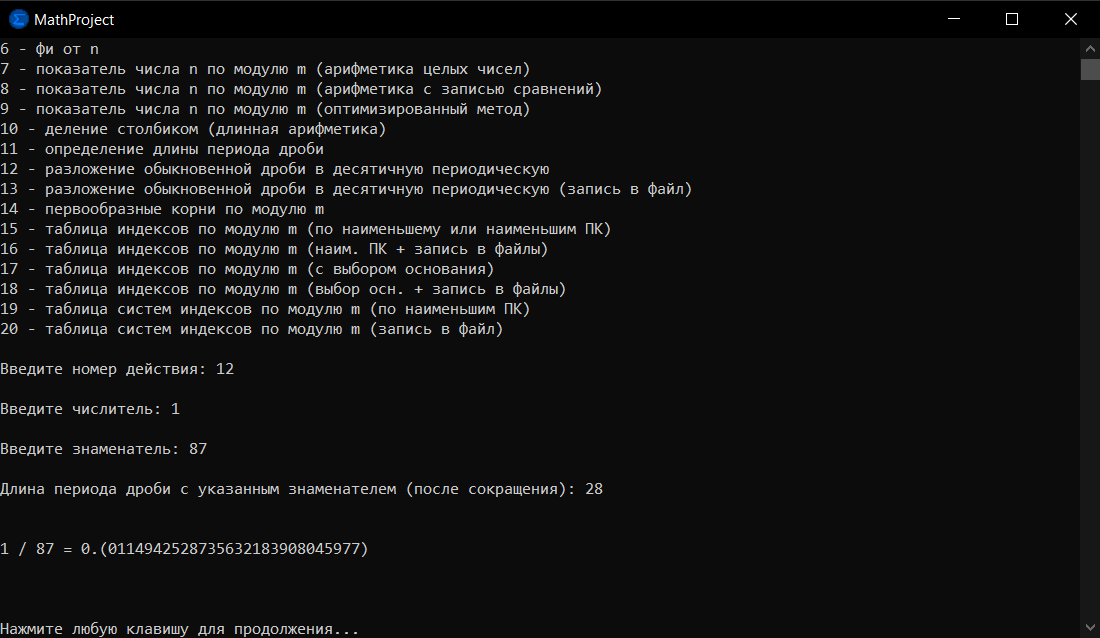
Рисунок 1. Перевод обыкновенной дроби в десятичную периодическую с помощью приложения, интерфейс программы

Пример 2: составим таблицу индексов по модулю 97 с помощью данного приложения. Выберем номер действия — 15. Далее введём значение m и таблица сразу будет построена.

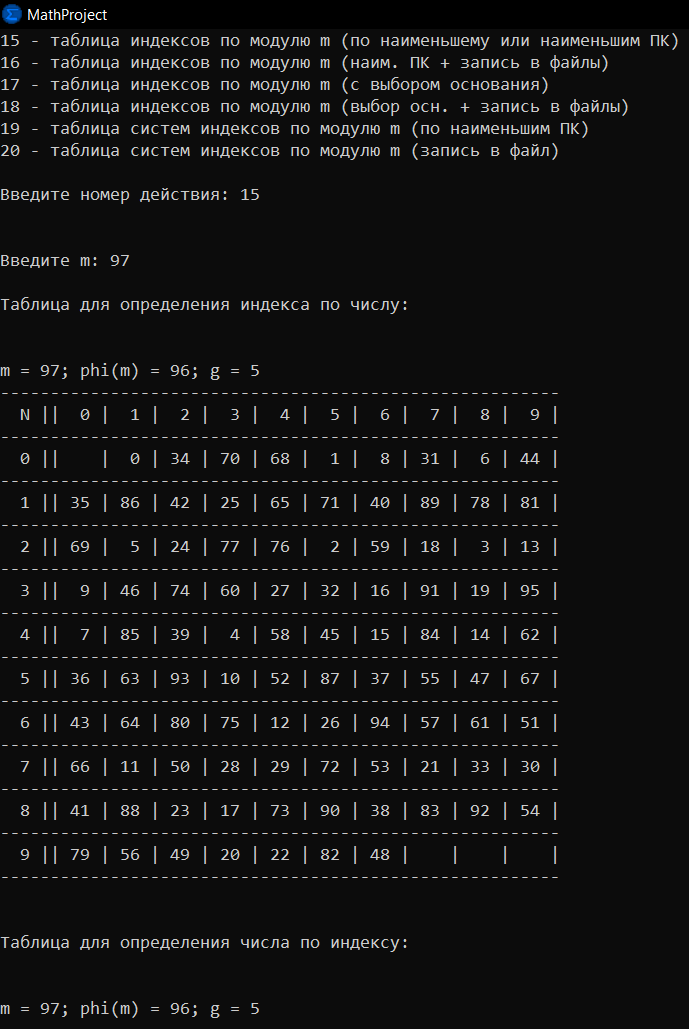
Рисунок 2. Построение таблицы индексов, часть 1

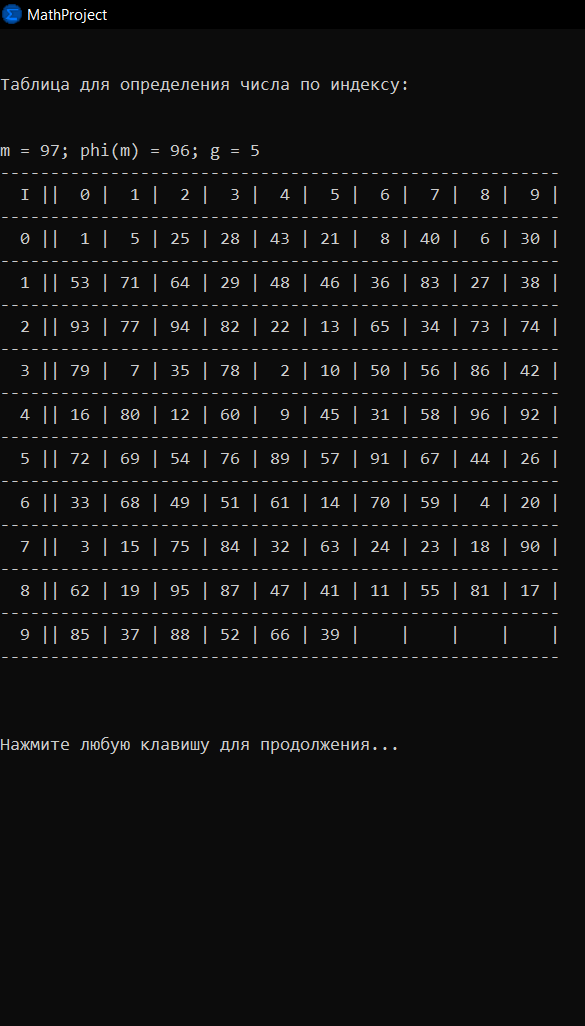
Рисунок 3.  Построение таблицы индексов, часть 2

Пример 2: составим таблицу индексов по модулю 24 с помощью данного приложения. Выберем номер действия — 15. Далее так же введём значение m и таблица будет построена.

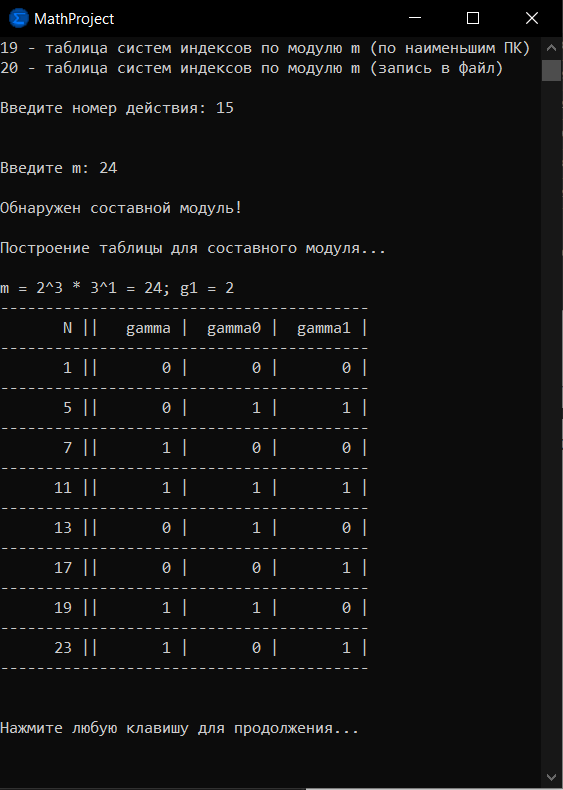
Рисунок 4. Составление таблицы индексов по составному модулю

Чтобы скачать данное приложение, вы можете воспользоваться следующими QR-кодами:

Рис. 5. QR-код версии приложения для Windows

Рис. 6. Исходный код приложения в qit-репозитории