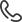Табурет Чебышева
Данная статья исследует разнообразные аспекты механики машин, сосредотачивая внимание на применении математических механизмов в различных областях, включая промышленность, сельское хозяйство, транспорт и быт. Описываются инновационные инженерные решения, такие как табурет Чебышева и инверсорные механизмы, их функциональные возможности и влияние на повседневную жизнь. Анализируются их вклад в развитие технического прогресса и математической физики.
До середины XIX века механика машин была преимущественно описательной наукой. Однако с течением времени начали использоваться аналитические, графические и экспериментальные методы исследования в этой области. Теория машин стала разделяться на различные направления, включая описательное машиноведение и теорию паровых машин. В конце века появилось самостоятельное направление – учение о деталях машин. Также произошло усложнение и расширение теории механизмов, включая кинематику механизмов и кинематическую геометрию [1]. Теория шарнирных механизмов и учение о строении механизмов стали важными областями исследований. С появлением зубчатых передач развивалась теория зубчатых передач, и были разработаны приближенные методы расчета ременных и цепных передач. В области динамики машин стали важными теория трения и теория автоматического регулирования к началу XX века [2].
В кинематике рычаг Чебышева - это четырехзвенный рычаг, который преобразует вращательное движение в приближенное линейное.
Он был изобретен математиком 19 века Пафнутием Чебышевым, который изучал теоретические проблемы кинематических механизмов. Одной из проблем была конструкция рычага, преобразующего вращательное движение в приближенное прямолинейное движение (прямолинейный механизм). Это также было изучено Джеймсом Уаттом в его работе "Усовершенствования парового двигателя", результатом которой стала связь Уатта.
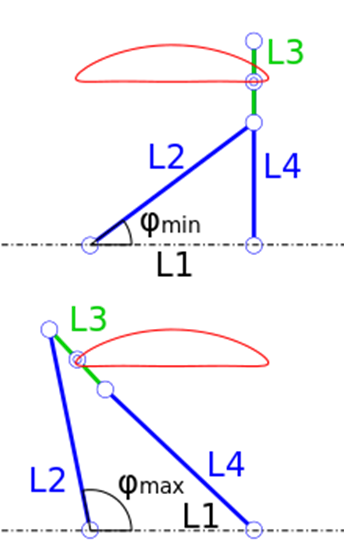
Рис. 1. Иллюстрация ограничений
Движение рычага может быть ограничено входным углом, который может изменяться с помощью скоростей, усилий и т.д. Входными углами могут быть либо связь L2 с горизонталью, либо связь L4 с горизонталью. Независимо от входного угла, можно вычислить движение двух конечных точек для звена L3, которые мы назовем A и B, и средней точки.
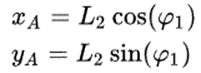
в то время как движение точки B будет вычисляться под другим углом,
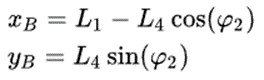
И, в конечном счете, мы запишем выходной угол в терминах входного угла,
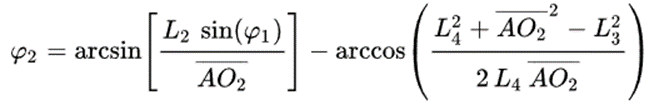
Следовательно, мы можем записать движение точки P, используя две точки, определенные выше, и определение средней точки.
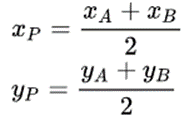
Механизм выставлялся на нескольких выставках, затем хранился в Science Museum (Лондон, Великобритания). В 1933 году механизм был передан в Imperial College of Science & Technology. Дальнейшая судьба неизвестна.
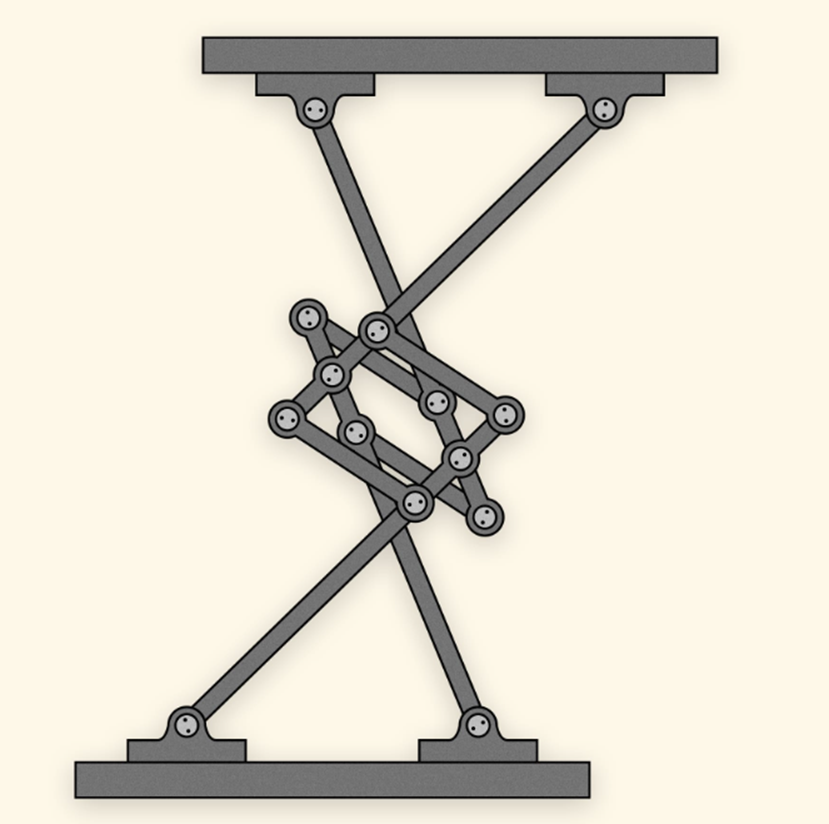
Рис. 2. Схематическое изображение Табурета Чебышева [3]
Табурет Чебышева нашел широкое применение в различных сферах, включая архитектуру, дизайн интерьеров и мебельное производство. Благодаря своей уникальной геометрии, он может служить стулом, журнальным столиком или подставкой для цветов [4]. Его компактные размеры помогают экономить место, а элегантный дизайн делает его привлекательным для различных интерьеров.
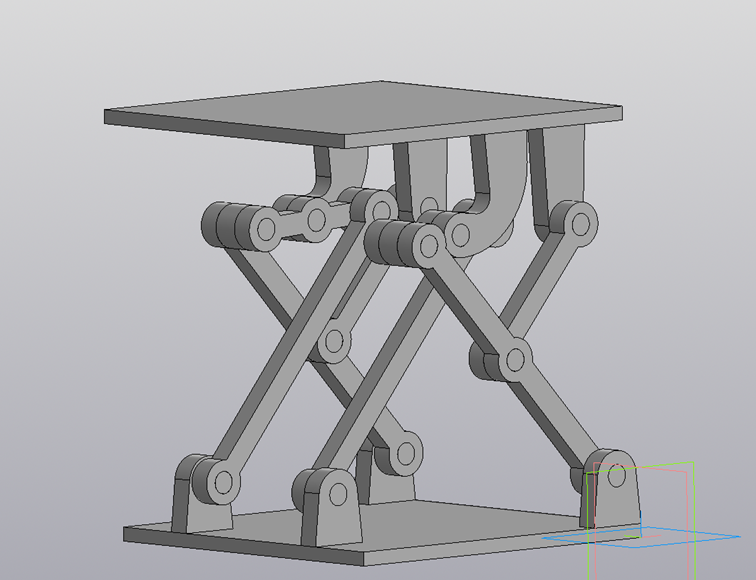
Рис. 3. 3D модель Табурета Чебышева
Но это не все – механизмы Пафнутия Львовича открывают увлекательный мир математической физики, особенно в области инверсорных механизмов. Эти механизмы нашли применение в различных устройствах, где необходима трансформация или сложное движение:
- В сельском хозяйстве они используются в механизмах сельскохозяйственных машин.
- В промышленности применяются в конвейерах и оборудовании для обработки материалов.
- В транспорте для изменения направления движения, переключения передач и торможения.
- В быту – в велосипедных механизмах и складной мебели.
Благодаря постоянному развитию и совершенствованию этих механизмов, наш мир становится более эффективным, удобным и инновационным. Взаимодействие между техническими науками и математикой продолжает расширять горизонты нашего понимания и вдохновляет на новые открытия и изобретения, формируя будущее технического прогресса.
- Ершов Б. А., Кутеева Г. А., Тарабарин В. Б. О роли моделей механизмов ПЛ Чебышева в истории науки и техники //Гуманитарный вестник. – 2016. – №. 1 (39). – С. 1.
- Горовенко Л. А., Сушков В. С. Некоторые аспекты проектирования механизмов стопоходящих роботов //Материалы IV Всероссийской конференции с международным участием (25-26 апреля 2019 г.). – 2019. – С. 107.
- Механизмы П.Л. Чебышева [Электронный ресурс]. – Режим доступа – URL: https://tcheb.ru/stool/1/ (Дата обращения: 05.10.23)
- Табурет Чебышева [Электронный ресурс]. – Режим доступа – URL: https://woodmod.livejournal.com/7736.html (Дата обращения: 05.10.23)