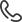Электромагнитные явления: обучение через решение инженерных задач

Тема «Электромагнитные явления» является ключевой в курсе физики для учащихся 11 классов, особенно для учащихся инженерного профиля. Понимание этой темы значительно влияет на их подготовку к обучению в техническом вузе и будущую профессиональную деятельность.

Будущие инженеры  должны понимать физическую сущность данного явления, поскольку явление электромагнитной  индукции применяется на практике — от проектирования электрических машин до разработки сенсоров и устройств, использующих электромагнитные поля.

Одной из эффективных методик обучения является решение инженерных задач, которые способствуют более глубокому пониманию физической теории, развитию критического мышления и инженерного подхода у учащихся.

В рамках программы дополнительного образования «Решение технических задач» при изучении темы «Электромагнитная индукция» большое внимание уделяется  задачам на движение перемычки с током в магнитном поле по П-образному контуру, данная конструкция лежит в основе линейных электромоторов и генераторов.

В процессе обучения учащиеся должны анализировать условие, строить математическую модель и анализировать ее.

Рассмотрим несколько примеров задач, рассматриваемых в процессе обучения.

До какой максимальной скорости может разогнаться проводник массой m, движущийся по длинным рельсам, не теряя контакта с рельсами. Коэффициент трения между проводником и рельсами равен µ. Проводник замкнут на источник тока с ЭДС ε и внутренним сопротивлением r. В пространстве между ними создано вертикальное магнитное поле (направление выбрано так, чтобы проводник двигался в направлении от источника тока) с индукцией B. Длина проводника l, его сопротивление R и намного больше внутреннего сопротивления источника. Сопротивление участков рельсов пренебрежимо мало. Ускорение свободного падения g.

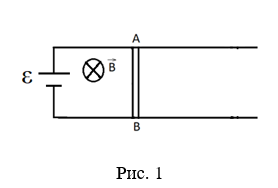
Проанализируем физическое явление. В задаче рассматривается полная замкнутая электрическая цепь. В этой цепи существуют два источника с ЭДС разной природы.

В задаче задан постоянный источник тока с ЭДС ε и внутренним сопротивлением r. Следовательно, за счет данного источника по контуру идет электрический ток от «+» к «-» источника тока (в нашей задаче по часовой стрелке). По проводнику АВ идет ток от контакта А к контакту В. Проводник с током находится в постоянном магнитном поле, индукция B которого направлена от наблюдателя.

На проводник с током в магнитном поле действует сила Ампера, направление которой определяется по правилу левой руки. Сила Ампера, действующая на проводник с током в магнитном поле, направлена вправо. Под действием этой силы проводник начнет удаляться от источника тока. В результате явления электромагнитной индукции создается ЭДС индукции ε_i. Физической причиной, вызывающей появление ЭДС индукции, является сила Лоренца F_л. Направление действия силы Лоренца на заряды, движущиеся внутри проводника вместе с ним (положительно заряженные ионы в узлах кристаллической решетки), определяем по правилу левой руки. Сила Лоренца направлена от контакта В к контакту А.

Изобразим эквивалентную замкнутую цепь, содержащую два источника ε, но разной природы.

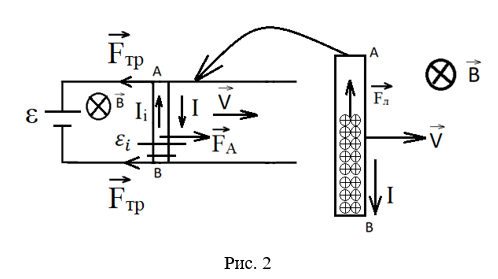
Основной идеей решения является описание физического явления в замкнутом контуре с учетом действия двух ЭДС ε.

Запишем закон Ома для полной цепи

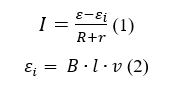
– ЭДС индукции ε_i в проводниках, движущихся в магнитном поле.

Знаки ε источника и ε_i – ЭДС индукции не совпадают.

Определим все силы, действующие на проводник с током, помещенный в однородном магнитном поле:

F_А – сила Ампера (направлена вправо);

F_тр – сила трения, направлена в противоположную сторону F_л (против движения проводника);

N – сила нормальной реакции опоры, направлена перпендикулярно опорам вверх;

mg – сила тяжести, направлена перпендикулярно плоскости чертежа вниз.

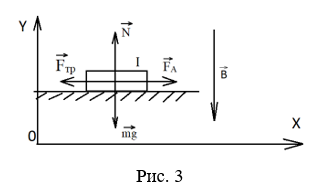
По второму закону Ньютона:

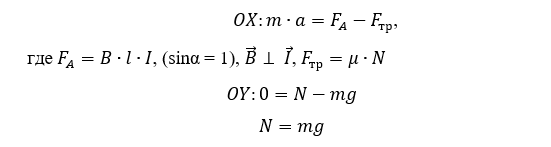
Решая систему уравнений, получаем

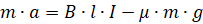
По условию задачи стержень должен достичь максимальной скорости, функция достигает максимума в том случае, если ее производная равна нулю. Производной от скорости по времени является ускорение. Значит, в тот момент, когда скорость достигнет максимального значения, ускорение будет равным нулю 

Отсюда следует

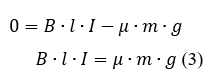
Подставим (1) в (3)

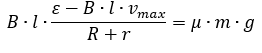
Выразим из данного уравнения 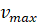 – максимальную скорость.

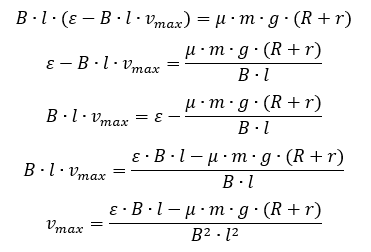
Проанализируем полученный результат. При движении проводника с током в магнитном поле произошло преобразование электрической энергии в механическую. Проводник разгоняется до максимальной скорости в магнитном поле, при этом электрическая энергия преобразуется в максимальную кинетическую энергию. Т.к. проводник обладает сопротивлением, можно рассмотреть преобразование электрической энергии не только в механическую, но и в тепловую, которую можно посчитать по закону Джоуля-Ленца. Также при решении данной задачи можно определить КПД установки

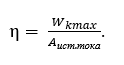
Особый интерес представляют задачи рассматривающие зарядку конденсатора за счет торможения перемычки, движущейся в магнитном поле по двум параллельным проводникам.

Рассмотрим зарядку конденсатора емкостью С, за счет торможения перемычки, движущейся в магнитном поле по горизонтальным сверхпроводящим рельсам со скоростью 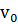. Длина перемычки l, ее масса m. Перемычка замкнута на конденсатор. Вся система находится в вертикальном магнитном поле с индукцией 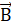. Сопротивление перемычки равно R. Трение перемычки о рельсы пренебрежимо мало. Найти силу тока зарядки конденсатора в самом начале торможения, максимальный заряд, приобретенный проводником при торможении.

Проанализируем физическое явление. В задаче представлен замкнутый контур, в котором перемычка АВ движется в магнитном поле со скоростью 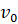. Перемычка движется по сверхпроводящим рельсам без трения. Система замкнута на конденсатор С. В начальный момент времени конденсатор не заряжен. В результате явления электромагнитной индукции в проводнике, движущемся в магнитном поле, создается ЭДС индукции, что является причиной появления в перемычке индукционного тока.

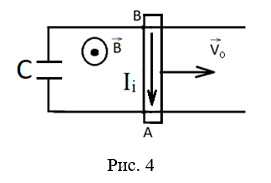
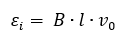
– ЭДС индукции ε_i в проводниках, движущихся в магнитном поле.

От скорости движения проводника зависит величина ε_i – ЭДС индукции, а значит и величина индукционного тока во время зарядки конденсатора.

Решение начнем с определения силы тока зарядки конденсатора в самом начале торможения. Для этого воспользуемся законом Ома для замкнутой цепи:

где 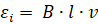 – ЭДС индукции, созданная в проводнике, движущемся в однородном магнитном поле;  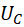– напряжение, созданное на конденсаторе.

Тогда 

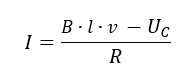
Рассмотрим полученное выражение в начальный момент времени, когда конденсатор еще не заряжен (мгновенно конденсатор зарядиться не может)

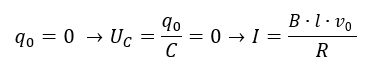
Данное выражение определяет силу тока в самом начале торможения.

Тормозящий проводник способен зарядить конденсатор.

Далее определим максимальный заряд конденсатора при торможении перемычки. Рассмотрим силу Ампера, действующую на перемычку, движущуюся в магнитном поле. Направление ее определим по правилу левой руки. В данной задаче сила Ампера направлена влево.

По второму закону Ньютона сила Ампера вызывает ускорение (F_тр = 0 по условию задачи). Сила Ампера направлена влево, а вектор ускорения совпадает с направлением силы Ампера. Значит, ускорение и начальная скорость противоположно направлены, и перемычка будет тормозить.

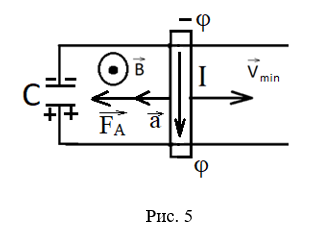
Запишем второй закон Ньютона:

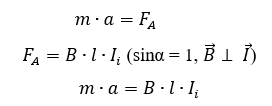
По определению проекция ускорения равна:

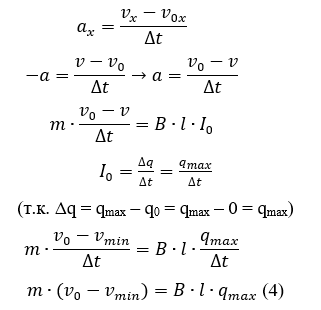
Видно, что изменение скорости связано с изменением заряда, при q = q_max →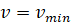

Как только конденсатор зарядится до максимального значения, ток в контуре станет равен нулю.

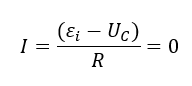
Отсюда следует

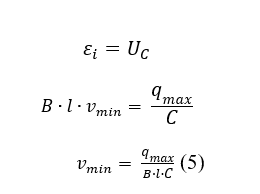
Подставим (5) в (4)

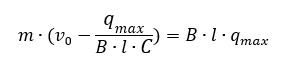
Теперь выразим q_max

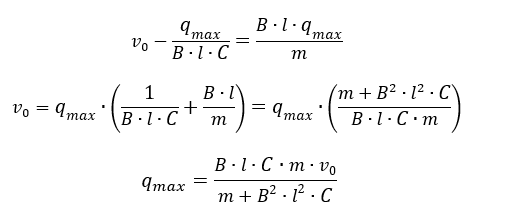
Проанализируем полученное решение. Чем больше начальная скорость перемычки, тем больший заряд может приобрести конденсатор при торможении перемычки в магнитном поле. Данная задача позволяет рассмотреть практическую сторону зарядки конденсатора при торможении движущегося в магнитном поле проводника. Кинетическая энергия проводника превращается в электрическую энергию конденсатора. При этом возможен и обратный процесс: конденсатор, разряжаясь, сможет преобразовать электрическую энергию вновь в механическую. По перемычке снова пойдет ток. Возникнет сила Ампера, которая заставляет проводник двигаться.

Обучение физике через решение инженерных задач является важным аспектом образовательного процесса. Учащиеся видят, как абстрактные физические законы применяются в реальных ситуациях, что способствует более глубокому пониманию материала. Когда студенты видят, как физика может быть связана с их интересами или будущей карьерой, это повышает их мотивацию и вовлеченность.

Кроме того, данный подход углубляет понимание теории, развивает практические навыки и критическое мышление.

1. Физика: Сборник контрольных заданий по электромагнитным явлениям для студентов инженерно-технических специальностей /П.А. Красных, В.М. Пауков, В.М. Полунин, Г.Т. Сычев; Под ред. В.М. Полунина; Курск. гос. техн. ун – т. Курск, 2000.
2. Н.П. Калашников, Т. А. Семёнова, В.Ф. Фёдоров. Руководство по решению задач по физике: Электричество и магнетизм: Учебное пособие. М.: НИЯУ МИФИ, 2014. — 424 с.
3. Гуревич А. Е. Физика. Электромагнитные явления. 8 кл.: Учеб. для общеобразоват. учеб. заведений. — М.: Дрофа, 1999. — 256 с.
4. Физика. Избранные задачи. Кн. II: Магнитное поле. Электромагнитная индукция. Электрический ток в среде. Электромагнитные колебания. Переменный ток в RCL-цепях. Электромагнитные волны. Оптика. Основы теории относительности. Квантовая физика/ Ю.Т. Павленко. — М.: Издательство «Экзамен», 2008. — 430, [2] с