Решение краевой задачи, с помощью основанных на физике нейронных сетей

С развитием нейронных сетей повысился интерес к использованию нейросетевых технологий для решения краевых задач, описываемых дифференциальными уравнениями в частных производных (ДУЧП). Этому способствовало широкое применение свободно распространяемых библиотек машинного обучения, реализующих автоматическое дифференцирование и алгоритмы обучения глубоких нейронных сетей. Нейросетевой подход представляется особенно эффективным по сравнению с традиционными методами для многомерных и/или нелинейных уравнений в частных производных и обратных краевых задач. В настоящее время сформировалось новое направления применения нейронных сетей — основанные на физике нейронные сети.

Идея основанных на физике нейронных сетей (PINN — physics-informed neural networks) были сформулирована в 2019 году в [1]. Концепция PINN была представлена как новый класс решателей, включающих математическую модель в структуру нейронной сети. Было использовано автоматическое дифференцирование, реализованное в библиотеках TensorFlow, PyTorch и других, проиллюстрирован подход PINN для решения нелинейных уравнений в частных производных, разработаны PINN, которые могут решать как прямые задачи, так и обратные задачи вычисления параметров модели.

Актуальные релизы системы MATLAB поддерживают автоматическое дифференцирование и создание пользовательских циклов обучения нейронных сетей (Custom Training Loop), включающих разработанные пользователем функции, например, нестандартные функции потерь, применяемые в PINN. Популярность MATLAB среди исследователей и инженеров, наличие большого количества математических и графических функций открывают большие возможности реализации PINN на MATLAB. Однако в настоящее время MATLAB практически не применяются для реализации PINN.  Недостаточно освещен этот вопрос в документации MATLAB [2], содержащей только пример решения одномерного уравнения. Целью данной работы является разработка и исследование алгоритма решения ДУЧП с помощью PINN, реализованной в системе MATLAB.

Основанные на физике нейронные сети позволяют решать ДУЧП, выраженные в наиболее общей форме

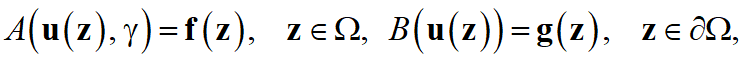
где 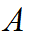 — дифференциальный оператор,  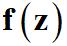— функция, определяющая данные задачи, 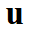— неизвестное решение, — вектор пространственно-временных координат,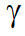 — параметры задачи,  — оператор краевых условий,  — граничная функция,  — область решения,   — граница области решения.

В такой формулировке можно описать множество физических систем, включая как прямые, так и обратные задачи. Цель решения прямых задач — найти функцию 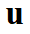 для каждого  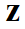, где   — заданные параметры. В случае обратной задачи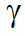  также должны быть определены из данных.

Решение задачи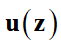 вычисляется с помощью нейронной сети, заданной вектором параметров  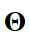. Нейронная сеть находит аппроксимацию решения  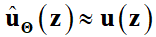, где 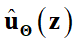  — приближенное решение, реализованное нейронной сетью с параметрами  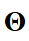. Причем в прямой задаче для вектора  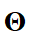 известны параметры  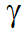, а для обратной задачи эти параметры подлежат определению. В процессе обучения нейронной сети вектор параметров находится путем минимизации функции потерь, которая зависит от дифференциального оператора, краевых условий и, возможно, от некоторых известных данных

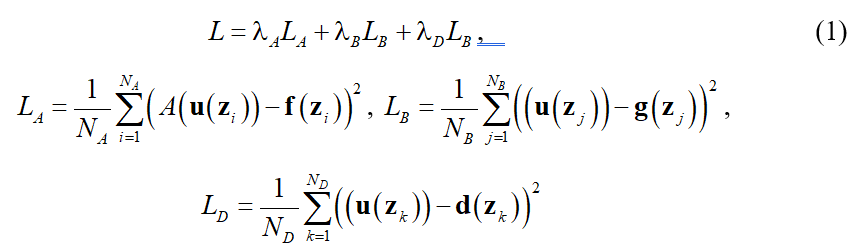
— суммы квадратов невязок в пробных точках внутри, на границе области решения и, возможно, в точках задания дополнительных условий, 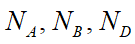  — количество пробных точек для уравнения, краевых условий и дополнительных условий,  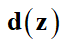 — функция дополнительных условий; — задаваемые пользователем весовые коэффициенты, регулирующие вклад разных составляющих в функцию потерь.

Для исследования реализации PINN в MATLAB целесообразно использовать полносвязные нейронные сети прямого распространения. В качестве функции активации исследуем   гиперболический тангенс, логистическую функцию и ReLu. Используем популярный быстрый алгоритм с адаптивной скоростью обучения Adam. Для сравнения используем стохастический градиентный спуск. Предложенный авторами алгоритм решения ДУЧП в MATLAB с помощью PINN состоит из следующих основных шагов.

1. Задание формы области решения и генерация псевдослучайных пробных точек внутри и на границе области решения. Для генерации пробных точек целесообразно использовать реализованную в MATLAB квазислучайную последовательность Соболя [3]. Точки, сгенерированные с помощью последовательности Соболя, в среднем распределены в области решения и на границе гораздо равномернее, чем для псевдослучайных последовательностей, генерируемых стандартными датчиками случайных чисел.
2.  Преобразование массива пробных точек в массив глубокого обучения (dlarray) системы MATLAB. Массив глубокого обучения хранит данные с дополнительными метками формата данных для настраиваемых циклов обучения и позволяет функциям вычислять и использовать производные путем автоматического дифференцирования.
3.  Задание структуры нейронной сети.
4. Инициализация сети с использованием лучшей в настоящее время инициализации Хе (He Initialization) [4], реализованной в MATLAB.
5. Задание алгоритма обучения сети и параметров алгоритма. В качестве основного алгоритма обучения выбран быстрый алгоритм с адаптивной скоростью обучения Adam. Для сравнения использован также алгоритм стохастического градиентного спуска с моментом. Имеющиеся в MATLAB алгоритмы обучения реализуют автоматическое дифференцирование.
6. Формирование функции потерь (1). 
7. При наличии графических ускорителей необходимо задать опцию использования GPU и некоторые массивы преобразовать в тип GPU.
8. Реализация пользовательского цикла обучения (Custom Training Loop). В каждой итерации пользовательском цикле (эпохе обучения) вычисляется функция потерь, с помощью автоматического дифференцирования вычисляется вектор градиента функции потерь. Обновляется скорость обучения. С помощью выбранного метода глубокого обучения настраиваются параметры сети. В пользовательский цикл обучения был добавлен вывод графика обучения в логарифмическом масштабе.

В Deep Learning Toolbox реализованы градиентные алгоритмы обучения первого порядка, использующие в процессе обучения градиент функции потерь по параметрам сети. Было также реализовано обучение сети с помощью функции fmincon, входящей в Optimization Toolbox, использующей квазиньютоновский алгоритм Бройдена-Флетчера-Голдфарба-Шанно с ограниченной памятью (L‑BFGS) [5]. При использовании функции fmincon критерием окончания итераций является значение меры оптимальности первого порядка (First-Order Optimality Measure). В нашем случае First-Order Optimality Measure вычисляется как бесконечная норма вектора градиента функции потерь.

Для исследования разработанных алгоритмов обучения была выбрана модельная задача, описываемая уравнением Пуассона

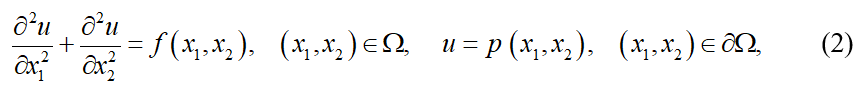
где   — граница области;  .

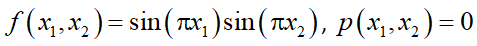В качестве области решения был выбран квадрат [0, 1]². С использованием последовательности Соболя было сгенерировано 100 пробных точек внутри области решения и 40 точек на границе.

С использованием разработанного алгоритма обучения решалась задача (2) с применением алгоритмов стохастического градиентного спуска с моментом и алгоритма Adam для различного числа слоев, числа нейронов в каждом слое и различных функций активации. Исследовались сигмоидальная функция активации (sigmoid), гиперболический тангенс (tanh) и ReLU — rectified linear unit. В результате каждого эксперимента вычислялось среднеквадратическое значение функции потерь (RMSE). Сеть обучалась до достижения среднеквадратического значения функции потерь, равного 0.01. По количеству эпох обучения сравниваемые алгоритмы обучения и функции активации дали близкие результаты. Лучшие результаты дали сети с небольшим числом слоев (3–4) и достаточно большим числом нейронов в каждом слое (50–100), обучаемые алгоритмом Adam. На рисунке 1 показан пример графика обучения.

Рисунок 1. График обучения (алгоритм Adam, сеть из 6 слоев по 30 нейронов)

Было также реализовано обучение сети с использованием алгоритма Бройдена-Флетчера-Голдфарба-Шанно с ограниченной памятью (L‑BFGS). Эксперименты проводились с сетями с функцией активации гиперболический тангенс. Обучение заканчивалось при значении First-Order Optimality Measure, не превышающем 10^-3. Эксперименты показали, что алгоритм успешно обучает нейронные сети с небольшим числом слое. Например, для сети с 4 слоями и 10 нейронами в каждом слое за 9056 итерации достигнуто среднеквадратическое значение функции потерь равно 4.436277e-04. В то же время, сети с большим числом слоев долго обучаются алгоритмом L-BFGS.

Эксперименты показали, что MATLAB может успешно применяться для реализации physics-informed neural networks. MATLAB позволил решить уравнение Пуассона до среднеквадратического значения функции потерь, равного 0.01. Лучшие результаты дали сети с небольшим числом слоев (3–4) и достаточно большим числом нейронов в каждом слое (50–100).

1. Raissia M., Perdikarisb P., Karniadakisa G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations // Journal of Computational Physics. — 2019, vol. 378. — P. 686–707.
2. Beale M.H., Hagan M.T., Demuth H.B. Deep Learning Toolbox. User Guide. — Natick, MA: MathWorks, Inc.,  2022. — 4112 p.
3. Белов А.А., Калиткин Н.Н., Тинтул М.А. ненадежность известных генераторов псевдослучайных чисел // Журнал вычислительной математики и математической физики. — 2020, том 60. — № 11. — С. 1807–1814.
4. He K., Xiangyu Z., Shaoqing R., Jian S. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification // Proceedings of the 2015 IEEE International Conference on Computer Vision. — 2015. — P. 1026–1034.
5. Кохендерфер М.Дж., Т. Уилер Т.А. Алгоритмы оптимизации. — СПб.: ООО "Диалектика", 2020. — 528 с.