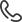Применение корреляционного и регрессионного анализа в системе прогнозирования технологического процесса

Введение

В любой отрасли одной из статей затрат является поддержание производственной инфраструктуры в рабочем состоянии. Применяемые меры для их снижения находятся в области оптимизации расходов на ремонты и техническое обслуживание производственного оборудования.

Для эффективной эксплуатации промышленного оборудования, минимизации затрат на техническое обслуживание и ремонты, а также ликвидации последствий их аварийной остановки, необходима своевременная и точная диагностика технического состояния в процессе эксплуатации.

Современные технические средства направленны на периодический или постоянный контроль парка оборудования, которые отслеживают задаваемый диапазон границ предельно-допустимых значений и при их нарушениях сигнализируют об этом, в дополнение возможна остановка оборудования или технологического процесса. То есть постоянный мониторинг с целью прогнозирования возможных проблем на ранних стадиях не выполняется.

Более актуальным и эффективным подходом будет является метод, основанный на прогнозе технического состояния и оценке рисков, состоящий из сбора и анализа специфичных данных с использованием алгоритмов и моделей. Эти модели основываются на анализах, корреляционном и регрессионном.

Определения и задачи анализов

Корреляционный анализ (корреляция) – статистический метод, позволяющий с использованием коэффициентов корреляции определить, существует ли зависимость между переменными и насколько она сильна. [1, с. 256]

Или, корреляционный анализ — это метод по изучению статистической зависимости между случайными величинами с необязательным наличием строгого функционального характера, при которой динамика одной случайной величины приводит к динамике математического ожидания другой.

Регрессионный анализ (регрессия) – это статистический метод, который связывает зависимую переменную с одной или несколькими независимыми (объясняющими) переменными. Это инструмент для количественного определения значения одной переменной на основании другой. Регрессия полезна для прогнозирования ответа на новые условия. [1, с. 269]

Задачами корреляционного анализа являются получение данных от объекта исследования (наблюдения) и определение зависимости между показателями данных. Также данный метод выявляет факторы, которые наиболее влияют на максимально благоприятный результат и изучает параметры связи при работе для наилучшей оценки производства.

Задача регрессионного анализа – выявление показателя, насколько изменение одной переменной (фактора) в среднем влияет на изменение другой переменной (результативного признака), выбор типа модели (формы связи), определение расчетных значений зависимой переменной (функции регрессии). Этот метод позволяет предсказывать значения зависимой переменной на основе значений независимых переменных. [2, с. 57]

То есть, при использование данных анализов, мы графически можем увидеть перемены одних данных при изменении других. А также насколько эти перемены, если они взаимосвязаны, располагаются в диапазоне положительной или отрицательной динамики.

Простыми словами, если мы хотим получить максимально благоприятный результат от системы диагностирования технического состояния промышленного оборудования или производственного процесса в целом, мы должны учитывать и применять методы корреляции и регрессии, так как мы должны учитывать возможное развитие последствий при изменении показателей, применяемых нами или не зависящих от нас.

Структура корреляционного анализа

Корреляционный анализ основывается на понятии коэффициента корреляции. Коэффициент корреляции может принимать значения от -1 до +1. Если коэффициент будет иметь значение вблизи +1, это означает, что две переменные имеют положительную линейную связь (прямая зависимость), т.е. при увеличении одной переменной, другая тоже увеличивается. При значении коэффициента вблизи -1, они имеют отрицательную линейную связь (обратная зависимость), при увеличении одной переменной, другая уменьшается.Возможна также ситуация, когда статистическая взаимосвязь отсутствует (отсутствие зависимости), коэффициент тогда близок к нулю (рис.1).

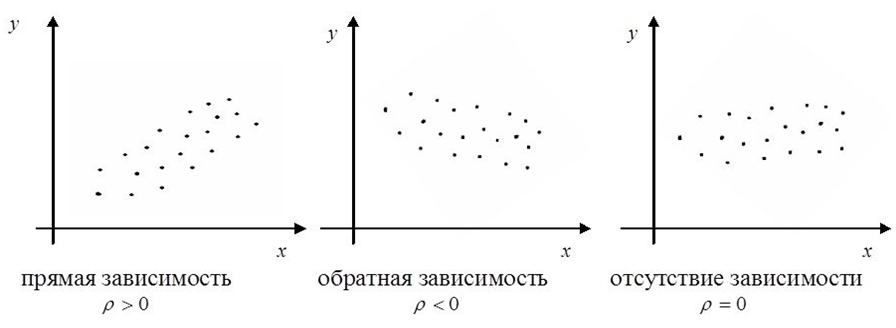
Рис.1 – Графики корреляционного поля

По форме связь делится на прямолинейную — равномерные изменения одного признака со­ответствуют равномерным изменениям второго признака при незначительных отклонениях. И криволинейную — равномерные изменения одного признака, со­ответствуют неравномерным изменениям второго признака, причем неравно­мерность имеет определенную закономерность. Общая тенденция в определен­ном моменте изменяет направление, дает изгиб.

Для проведения анализа используют следующие формулы:

Коэффициента линейной зависимости Пирсона:

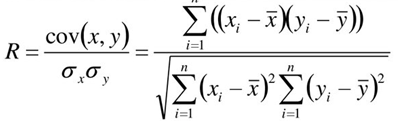
где: ,  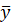 ― среднее значение выборок; x, y ― значения выборки; s_x, s_y, ― среднее квадратическое отклонение;

Ранговый коэффициент линейной корреляции Спирмена:

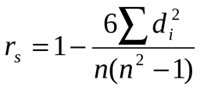
где: n — количество ранжируемых признаков (показателей, испытуемых); d — разность между рангами по двум переменным для каждого испытуемого; d² — сумма квадратов разностей рангов. [1, с.257-259]

Также корреляция может быть парной – существует зависимость между двумя признаками, один из которых – признак-результат или зависимая переменная, второй – признак-фактор или независимая переменная, и множественной, когда зависимость между одним признаком-результатом и двумя и более признаками-факторами. Показатели корреляции называются показателями или характеристиками тесноты корреляционной связи.

Поскольку корреляционная связь достаточно полно проявляется только в массе наблюдений, объем выборки данных должен быть большим, так как в этом случае сглаживается влияние других факторов.

Структура регрессионного анализа

В отличие от корреляционного анализа, который только отвечает на вопрос, существует ли связь между анализируемыми признаками, регрессионный анализ дает и ее формализованное выражение.

Регрессионный анализ может дать оценку размера и направления связи, а также тесты статистической значимости, доверительные интервалы и прогнозы будущих результатов.

Чтобы получить глубокое понимание регрессионного анализа, необходимо сначала разобраться в следующих терминах:

Зависимая переменная — это переменная, которую вы хотите проанализировать или спрогнозировать. Это переменная результата, которую вы пытаетесь понять и объяснить.

Независимые переменные — это переменные, которые, по вашему мнению, влияют на зависимую переменную. Их часто называют переменными-предсказателями, поскольку они используются для прогнозирования или объяснения изменений в зависимой переменной.

При рассмотрении зависимости двух случайных величин говорят о парной регрессии, зависимость нескольких переменных называют множественной регрессией.

Для построения регрессионного анализа используется графический метод, прямоугольная система координат, оси которой соответствуют обеим переменным. На таком графике каждый объект представляет собой точку, координаты которой заданы значениями двух переменных. Уже по самой конфигурации полученной области заполнения, по геометрии множества точек можно судить и предполагать о характере связи между двумя переменными.[4]

Регрессия позволяет подобрать к этим точкам линию у=f(x), которая вычисляется по методу наименьших квадратов и даёт максимальное приближение к заданным параметрам (рис.2).

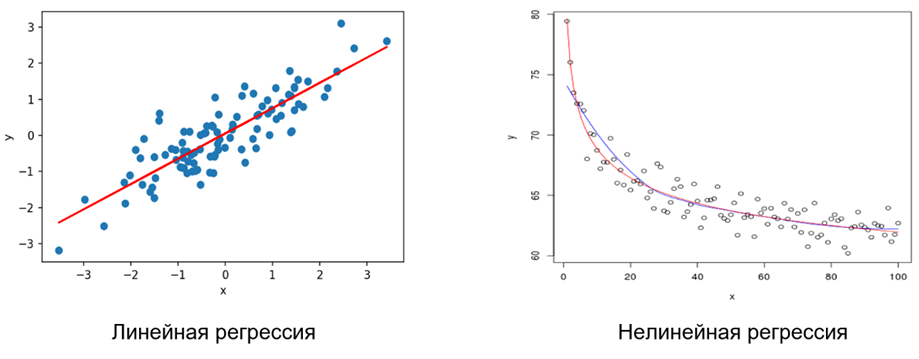
Рис.2 – Графики данных регрессии

Линейная регрессия — модель зависимости переменной x от одной или нескольких других переменных (факторов, регрессоров, независимых переменных) с линейной функцией зависимости. Одним из его достоинств является лёгкость интерпретации результатов.

Линейная регрессия некоторой зависимой переменной y на набор независимых переменных x = (x₁, …, xᵣ), где r – это число предсказателей, предполагает, что линейное отношение между y и x:

y = 𝛽₀ + 𝛽₁x₁ + ⋯ + 𝛽ᵣxᵣ + 𝜀, где 𝛽₀, 𝛽₁, …, 𝛽ᵣ – коэффициенты регрессии, 𝜀 – случайная ошибка.

Линейная регрессия вычисляет оценочные функции коэффициентов регрессии или просто прогнозируемые весы измерения, обозначаемые как b₀, b₁, …, bᵣ. Они определяют оценочную функцию регрессии:

f(x) = b₀ + b₁x₁ + ⋯ + bᵣxᵣ.

Эта функция захватывает зависимости между входами и выходом достаточно хорошо.

Для каждого результата наблюдения i=1, …, n, оценочный или предсказанный ответ f(xᵢ) должен быть как можно ближе к соответствующему фактическому ответу yᵢ. Разницы yᵢ − f(xᵢ) для всех результатов наблюдений называются остатками. Регрессия определяет лучшие прогнозируемые весы измерения, которые соответствуют наименьшим остаткам. [1, с. 270]

Нелинейная регрессия — это способ нахождения нелинейной модели взаимосвязи между зависимой переменной и набором независимых переменных:

y = f (X, β) + ϵ, где f — функция регрессии, ϵ — член ошибки, а X, β - параметры вектора.

В отличие от традиционной линейной регрессии, которая ограничена оценкой линейных моделей, нелинейная регрессия может оценивать модели с произвольными взаимосвязями между независимыми и зависимыми переменными. Это достигается при помощи итерационных алгоритмов оценки. [3, с. 324]

Одним из главных преимуществ нелинейной регрессии является ее способность моделировать сложные нелинейные зависимости. Линейная регрессия ограничена линейными функциями, в то время как нелинейная регрессия может аппроксимировать более сложные формы зависимости, такие как параболы, экспоненциальные функции, логарифмические функции и другие. Например, в экспоненциальной модели параметр может представлять собой коэффициент увеличения или уменьшения вероятности, а не просто изменение величины.

Корреляционно-регрессионная модель на производстве

Для каждого отдельного производственного процесса источники массивов данных могут различаться в зависимости от специфики производства.

Для применения корреляционного и регрессионного анализа необходимо получить данные производственного процесса с минимальным уровнем искажений в условиях, близких к идеальным. Такие данные требуются для расчета максимально возможного уровня отклонений для производственного процесса.

Затем необходимо установить предельно допустимые значения, с помощью нормативов производства, для каждого датчика промышленного оборудования. Но данные нормативов, заданные на бумаге, могут отличаться от реальных данных, из-за особенностей производственного оборудования, а также внешних факторов, условий эксплуатации и т. д.

Чтобы понимать границы допустимых значений для совокупности данных с приборов-показателей, требуется определить максимально допустимый уровень отклонений для них. Чтобы такой уровень был максимально достоверным, его необходимо устанавливать при максимальном контроле за производственным процессом для снижения вероятности возникновения ошибок и несанкционированных действий. Такие данные будут базовыми. Их можно использовать при анализе данных при стандартных условиях производственного цикла.

В дальнейшем отчетные данные по производственному процессу в ходе корреляционного и регрессионного анализа будут сравниваться с подобными данными для контроля возможных отклонений в производственном процессе. С помощью этих моделей можно выявлять износ конкретного оборудования, а также слабые звенья в взаимосвязи всех единиц производства.

При возникновение нестандартных ситуаций, когда нельзя остановить производственный процесс немедленно, программное обеспечение на цифровой платформе, основанная на регрессионной модели, поможет выбрать правильный ход действий, чтобы ускорить процесс принятия решений с целью исключения нежелательные последствия.

Таким образом достигается максимальная оперативность реагирования на инциденты.

Вывод

Применяемые анализы характеризуется следующими положительными результатами:

• выявление факторов, оказывающих наибольшее влияние на результативный признак;
• выявление неизученных ранее причин связей;
• построение корреляционной модели с ее параметрическим анализом;
• построение регрессионной модели с целью прогнозирования технического состояния и надежности реализации оборудования;
• исследование значимости параметров связи и их интервальная оценка.

1. Бююль А., Цеффель П. SPSS: искусство обработки информации. – М., 2005
2. Глинский В.В., Ионин В.Г. Статистический анализ: учеб. пособие. М.: ИНФРА-М, 2002.
3. Наследов А. IBM SPSS Statistics 20 и AMOS: профессиональный статистический анализ данных. – СПб., 2013
4. Регрессионный анализ – URL: https://pandia.ru/ – Текст: электронный.