ОПРЕДЕЛЕНИЕ ПОТЕРЬ ДАВЛЕНИЯ В ГАЗОВОМ ПОТОКЕ ЦИЛИНДРИЧЕСКОГО КАНАЛА

Введение

Определение потерь давления на трение является важнейшей задачей, возникающей при гидравлическом расчете трубопроводов всех типов. Основным инструментом для этих целей служит формула Дарси-Вейсбаха, главной составляющей которой является коэффициент гидравлического трения. Определению этого коэффициента посвящены работы [1 - 3], в которых приводится зависимость коэффициента трения от различных факторов и, прежде всего, от качества внутренней поверхности трубопровода. Столь пристальное внимание к коэффициенту гидравлического трения, безусловно, несколько преувеличено, так как существуют более информативные показатели движения газа в трубопроводах, зная которые, можно определить потери давления в канале. К таким показателям относятся отношение средней скорости к максимальной на оси канала (качество канала), коэффициент расхода и т.д. Поэтому возникает необходимость разработки более эффективной и менее затратной инженерной методики определения потери давления в канале.

Постановка цели и задач научного исследования

Целью данной работы является разработка методов расчета потерь давления газа в цилиндрическом канале. Кроме того, необходимо определить связь между полем скоростей в канале и коэффициентом гидравлического трения.

Для выполнения поставленной цели необходимо решить следующие научные задачи:

• во-первых, найти потерю полного давления в цилиндрическом канале с использованием политропного расширения газа в канале;
• во-вторых, определить взаимосвязь коэффициента расхода газа в канале с потерей полного давления;
• в-третьих, установить функциональную связь между полем скоростей и коэффициентом гидравлического трения в цилиндрическом канале.

Определение потерь полного давления газа в цилиндрическом канале с использованием политропных процессов газового потока

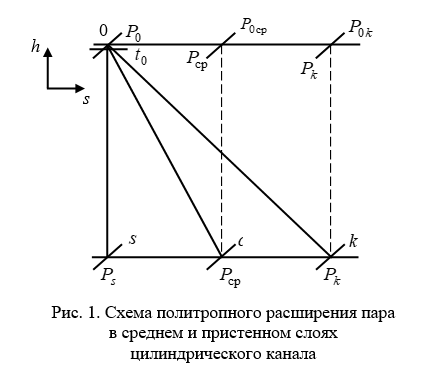
Рассмотрим процесс политропного расширения перегретого пара в диаграмме h,s (энтальпия - энтропия). Для этого изобразим схему расширения среднего и пристенного слоев газа в цилиндрическом канале (рис. 1) и определим изменение полного давления в процессе расширения. Для вывода формулы потерь полного давления запишем уравнения изотермы, изоэнтропы и политропы [1]:

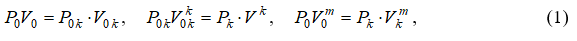
где 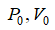  – давление и удельный объем перед каналом;

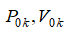      – полное давление и удельный объем в точке K пристенного слоя;

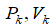       – давление и удельный объем в точке K пристенного слоя;

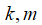          – показатели изоэнтропы и политропы;

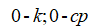 – политропные процессы расширения пара в пристенном и среднем слоях.

После некоторых преобразований зависимостей (1) получим

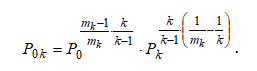
В работе [4] была получена следующая зависимость:

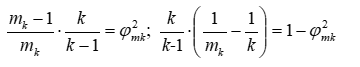
Тогда полное давление в точке K будет определяться следующим выражением:

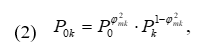
где 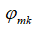 политропный коэффициент скорости пристенного слоя газа.

Из формулы (2) следует, что полное давление пристенного слоя газа будет определяться начальным и конечным давлением газа, а также политропным коэффициентом скорости этого слоя.

Разделив левую и правую части формулы (2) на 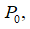 получим

Выразим потери полного давления в относительных единицах:

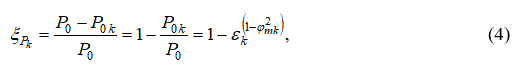
где 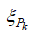 относительная величина потерь полного давления в пристенном слое.

Для i-го слоя газа потери полного давления будут определяться формулой

где 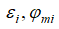 относительное противодавление и политропный коэффициент скорости i-го слоя газа соответственно. Поскольку каждый слой газа имеет свой политропный коэффициент скорости, то для оценки потерь полного давления в канале в целом введем осредненные параметры газового потока и, прежде всего, политропный коэффициент скорости среднего слоя. В работе [4] была определена функциональная связь между критическим давлением и критическим коэффициентом расхода пристенного слоя 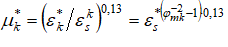, а в работе [5] получена зависимость для определения максимального коэффициента расхода пристенного слоя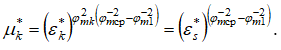 

Используя связь 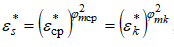, сравним обе зависимости и получим связь между политропными коэффициентами скорости разных слоев:

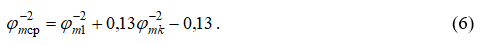
Потери полного давления в газовом потоке канала через параметры среднего слоя будут определяться следующей зависимостью:

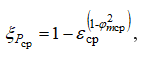
а через параметры пристенного слоя

где 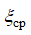 относительная величина потерь полного давления в среднем слое или в канале в целом.

Следует отметить, что потери полного давления в канале зависят от политропных коэффициентов скорости и от относительного противодавления за каналом 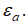Так как политропные коэффициенты скорости не зависят от относительного противодавления, то потери полного давления в канале достигнут максимального значения при 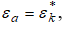то есть при критическом отношении давлений в пристенном слое. В работе [6] были определены границы начального, переходного и основного участков в газовом потоке цилиндрического канала значительной протяженности. Было получено, что на границе между переходным и основным участками устанавливается следующие параметры: в первом слое (на оси канала) 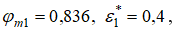в пристенном слое 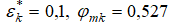и в среднем слое 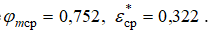Тогда потери кинетической энергии и полного давления в этих слоях будут следующие: на оси канала потери кинетической энергии 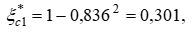полного давления 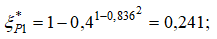в пристенном слое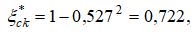 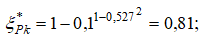в среднем слое 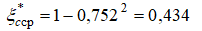и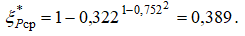 

Видно, что потери в газовом потоке цилиндрического канала до момента формирования параметров основного участка потока достигают значительных величин.

Определение связи между коэффициентом расхода газа в канале и потерей полного давления

В работе [5] было получено уравнение расхода газа через цилиндрический канал

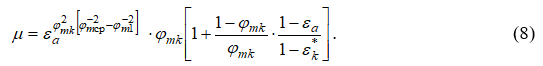
При достижении 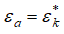 выражение (8) примет следующий вид:

где 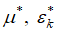 критический коэффициент расхода и критическое отношение давлений.

При критических параметрах газа на выходе из канала формула (7) примет следующий вид:

Разделив уравнение (9) на уравнение (10), получим

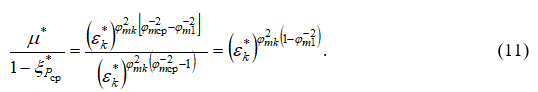
Проанализируем выражение (11). Для этого рассмотрим следующие варианты:

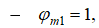тогда 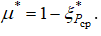Это будет происходить на начальном участке газового потока в цилиндрическом канале, когда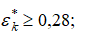 

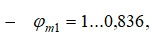 тогда 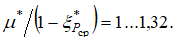Это соответствует переходному участку в канале и изменению критического отношения давлени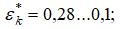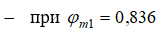й 

 и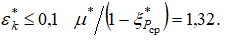 

Такое поведение данных зависимостей обусловлено следующими факторами. На начальном участке газового потока в цилиндрическом канале значительной протяженности, когда имеется изоэнтропийное ядро, критическое отношение давлений на оси канала остается неизменным и равным 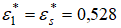. Неизменность критического давления на оси канала приводит к тому, что полезная доля полного давления канала полностью преобразуется в критический коэффициент расхода, то есть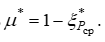 

Дальнейшее движение газа по каналу связано с уменьшением критического давления на оси канала, обусловленного действием сил молекулярной вязкости и турбулентным перемешиванием газа. Причем это воздействие усиливается по мере движения газового потока. Критическое отношение давления на оси канала уменьшается от 0,528 до 0,4. Все это происходит на переходном участке газового потока. Отношение 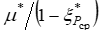изменяется в пределах 1…1,32 и равняется отношению критического давления при изоэнтропийном расширении к критическому давлению первого слоя, то есть 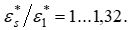Насколько понижается критическое давление первого слоя 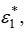настолько возрастает соотношение 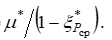Максимальная величина этого соотношения достигается на границе переходного и основного участков, ког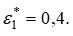да Тогда 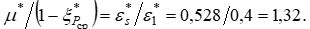На основном участке газового потока в цилиндрическом канале значительной протяженности 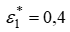и не уменьшается с уменьшением 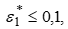поэтому отношение 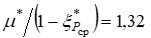остается неизменным. Если бы критическое давление на оси канала оставалось равным 0,528, то 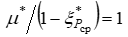на протяжении всех участков газового потока в канале.

Чтобы получить соотношение (11) не только для критических параметров, то есть когда 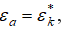, но и когда 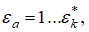, разделим уравнение (8) на уравнение (7), предварительно преобразовав его:

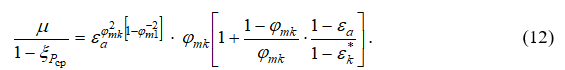
Данная формула справедлива для всех участков газового потока в цилиндрическом канале значительной протяженности. На начальном участке газового потока, когда 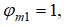формула (12) преобразуется и будет определять среднерасходный коэффициент скорости газового потока [5]

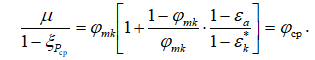
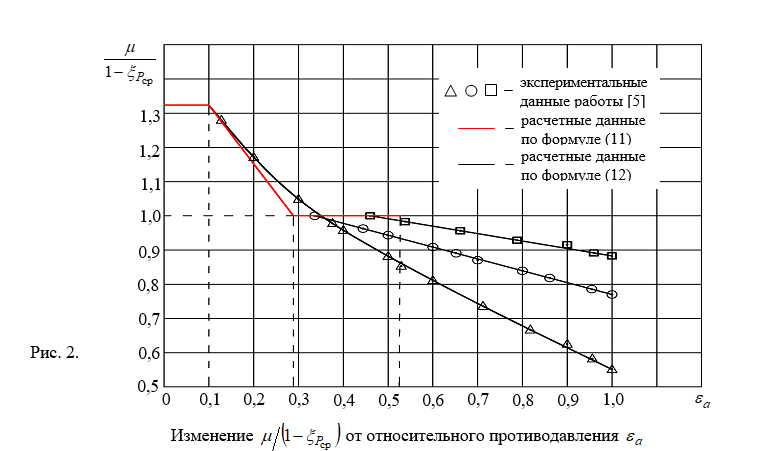
Для наглядности изменения 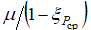 от 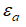построим графики функций, выражающихся уравнениями (11) и (12) (рис. 2), и нанесем на эти графики экспериментальные данные работы [5].

Из рис. 2 видно, что расчетные значения, полученные по формулам (11) и (12), и экспериментальные значения совпадают вполне удовлетворительно.

Определение функциональной зависимости между полем скоростей и коэффициентом гидравлического трения в цилиндрическом канале

В работе [3] была использована зависимость между гидравлическим коэффициентом трения λ и отношением средней скорости к максимальной 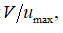 которая выражается следующей формулой:

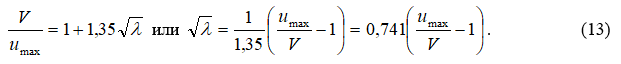
Основная задача состоит в том, чтобы определить, как изменяется 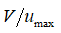 по радиусу цилиндрического канала. Большинство авторов работ по определению коэффициента гидравлического трения в трубопроводах работают в области основного участка и оперируют абсолютным значением скоростей: V, м/с – средняя скорость по сечению трубопровода, и  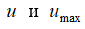м/с – текущая и максимальная скорости в поперечном сечении трубопровода на основном участке. В данной работе мы оперируем политропными коэффициентами скоростей:  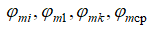текущей, первого, пристенного слоев и средним коэффициентом скорости. Эти переменные связаны друг с другом следующими соотношениями: 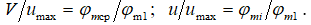. Тогда формула (13) примет следующий вид:

При разработке критических режимов течения газа была получена зависимость

где 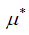 критический коэффициент расхода в канале. Подставив выражение (15) в формулу (14), получим

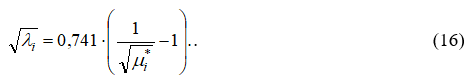
Для получения нужной зависимости требуется определить, как изменяется критический коэффициент расхода по радиусу канала. Для этого используем зависимость (6) применительно к критическому коэффициенту расхода. Тогда получим

где 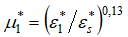 критический коэффициент расхода первого слоя [4];

      С_i – показатель степени координаты i-го слоя.

В соответствии с зависимостями работы [6] показатель степени определяется так:

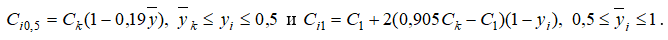
Здесь 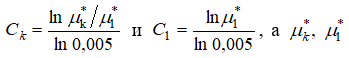 - критические коэффициенты расхода газа пристенного и первого слоев соответственно.

Подставив значение критического коэффициента расхода из формулы (17) в формулу (16), получим изменение коэффициента гидравлического трения по радиусу цилиндрического канала 

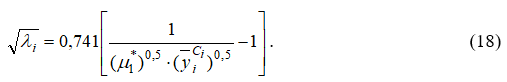
Вычислим изменение коэффициента гидравлического трения по радиусу трубопровода диаметром 350 мм, используя данные работы [3], а также 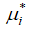по формуле (17) и отношение политропных скоростей 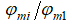работы [6]. Результаты расчетов сведем в таблице. Исходные данные для расчета: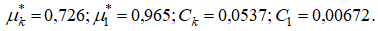 

На основании таблицы построим графики изменения гидравлического коэффициента трения по радиусу канала и по полю скоростей (рис. 3).

Таблица

Изменение коэффициента гидравлического трения по радиусу трубопровода диаметром 350 мм

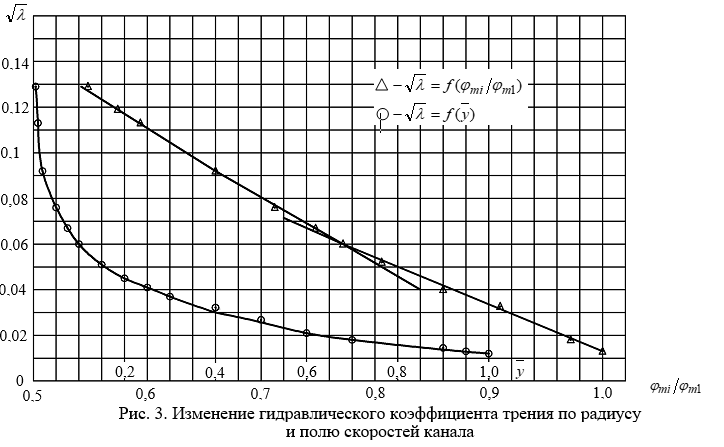
Из рис. 3 видно, что коэффициент гидравлического трения в пристенных слоях газового потока канала резко уменьшается, примерно до 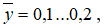, а затем переходит в стадию плавного уменьшения до величины коэффициента трения на оси канала. Изменение 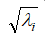по радиусу канала определяется уравнением (18). Что касается зависимости коэффициента трения от поля скоростей в канале, то видно, что эта зависимость линейная, но определяется двумя прямыми линиями, которые пересекаются между собой, меняя свой наклон в точке, в которой значение скоростей определяется ординатой  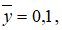то есть 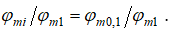Для этой точки также характерно то, что отношение значения коэффициента трения в ней 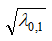к коэффициенту гидравлического трения пристенного слоя  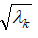- величина постоянная и равная 0,47.

Тогда уравнение первой прямой будет иметь следующий вид:

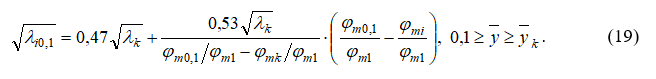
Уравнение второй прямой 

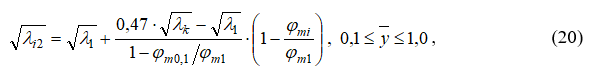
где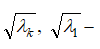 

коэффициенты гидравлического трения пристенного и первого слоев;

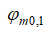 значение политропного коэффициента скорости при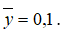

Уравнения (19) и (20) действительны для цилиндрических каналов на переходном и основном участках газового потока в канале.

Таким образом, установлена функциональную связь между полем скоростей и коэффициентом гидравлического трения в цилиндрическом канале.

Выводы

1. Разработана инженерная методика определения потерь полного давления в цилиндрическом канале с использованием политропных процессов расширения газа.
2. Определена зависимость между коэффициентом расхода и потерей полного давления в канале.
3. Установлена функциональная связь между полем скоростей и коэффициентом гидравлического трения в цилиндрическом канале.

1. Абрамович Г.Н. Прикладная газовая динамика / Г.Н. Абрамович. – М.: Наука, 1991. – 594 с.
2. Альтшуль А.Д. Гидравлика и аэродинамика / А.Д. Альтшуль, Л.С. Животовский, Л.П. Иванов. – М.: Стройиздат, 1987. – 414 с.
3. Альтшуль А.Д. Гидравлические потери на трение в трубопроводах / А.Д. Альтшуль. – М.-Л.: Госэнергоиздат, 196 – 256 с.
4. Сиваков В.И. Определение критических параметров реального (вязкого) газового потока по известному полю скоростей на выходе канала. Определение поля скоростей по известному критическому отношению давлений в пристенном слое газового потока канала / В.И. Сиваков // Научный аспект № 5 – 2024 (электронный ресурс).
5. Сиваков В.И. Определение расходов газа через канал при дозвуковых, смешанных и звуковых режимах течения газа / В.И. Сиваков // Международный журнал гуманитарных и естественных наук №8-2 (95) 2024 С. 179 - 185.
6. Сиваков В.И. Изменение профиля скоростей в газовом потоке цилиндрического канала значительной протяженности // Научные высказывания. 2024. №17 (64)