ФИЗИЧЕСКАЯ МОДЕЛЬ ВОЗНИКНОВЕНИЯ И РАЗВИТИЯ ЗВУКОВОЙ ПОВЕРХНОСТИ В ГАЗОВОМ ПОТОКЕ ЦИЛИНДРИЧЕСКОГО КАНАЛА

Введение

Одной из актуальных проблем современной газовой динамики являются вопросы определения критических режимов истечения реального газа через различные каналы. Существующая в настоящее время теория критических режимов истечения газа была разработана под руководством автора работы [1]. Основополагающие принципы этой теории изложены в работе [4]. Необходимо добавить, что на данный момент в газовую динамику введены и используются три критических отношения давлений: первое критическое отношение давлений, второе критическое отношение давлений, третье критическое отношение давлений. Все они предполагают возникновение замкнутой звуковой поверхности, которая опирается на выходные кромки канала. Следует особо отметить работу [3]. Автор провел анализ работ на эту тему за 100 лет. Это колоссальная работа. Проделал также научно-исследовательскую работу, но так и не ответил на вопрос. Как возникает и развивается линия перехода (звуковая поверхность через скорость звука)? И остался на позиции автора [1]. Ответ на этот вопрос дает наша статья, в которой изложены физические явления, сопровождающие возникновение и развитие звуковой поверхности в газовом потоке при сверхкритических перепадах давления на канал.

Постановка цели и задач научного исследования

Целью данной работы является определение возникновения и развития звуковой поверхности в газовом потоке цилиндрического канала. Для достижения поставленной цели необходимо решить следующие задачи: разработать физическую модель возникновения и развития звуковой поверхности; обосновать причины появления неравномерности статического давления на звуковой поверхности; определить смещение звуковой поверхности в газовом потоке цилиндрического канала.

Возникновение и развитие элементов звуковой поверхности в газовом потоке цилиндрического канала

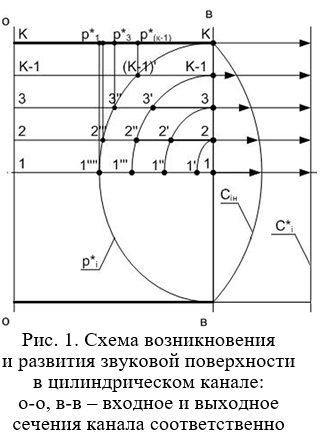
При определении критического расхода идеального газа через цилиндрический канал исходят из того, что во всем выходном сечении канала скорость газа достигает скорости звука одновременно и дальнейшее понижение давления за каналом не приводит к увеличению расхода газа. Этому явлению дано следующее объяснение. При критическом расходе газа в выходном сечении канала образуется звуковая поверхность или поверхность перехода, которая совпадает с выходным сечением канала, и понижение давления за каналом не может проникнуть внутрь канала, происходит так называемое явление «запирание» канала по расходу газа. Что касается критического (максимального) расхода реального (вязкого) газа через цилиндрический канал, то он тоже существует, при этом тоже образуется звуковая поверхность на выходе канала и происходит «запирание» канала. Но эта звуковая поверхность не совпадает с выходным сечением канала. С целью определить это положение рассмотрим физические явления, происходящие в газовой струе на выходе канала при сверхкритических перепадах давления на канале. Для этого изобразим на рис. 1 цилиндрический канал с произвольным начальным полем скоростей на выходе канала С_iн. Разобьем этот газовый поток на «К» слоев и рассмотрим, как изменяются термодинамические параметры газа в этих слоях при сверхкритических перепадах давлений на канале. По мере понижения давления газа за каналом и при постоянном давлении перед каналом скорость газа на выходе канала растет, и при некотором давлении 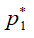 в слое 1-1 на оси струи она достигает местной скорости звука  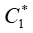в точке 1. Параметры газа в точке 1 называются критическими и при дальнейшем понижении давления газа за каналом остаются неизменными в силу постоянства геометрии канала. Дальнейшее понижение давления газа за каналом приводит к увеличению скорости газа в дозвуковой части струи, к росту расхода газа через канал и достижению скорости газа скорости звука в точке 2 газового слоя 2-2 и критического давления 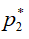. Поскольку между слоями 1-1 и 2-2 за сечением 1-2 в дозвуковой части этих слоев имеется разность давлений, так как 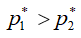, то произойдет понижение термодинамических параметров газа в дозвуковой части слоя 1-1 и увеличение скорости газа до скорости звука в точке 1, то есть происходит расширение газа в слое 1-1 навстречу потоку – внутрь канала. Расширение газа в слое 1-1 навстречу потоку будет происходить до тех пор, пока давление  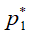слоя 1-1 не сравняется с давлением смежного слоя 2-2. В результате этого параметры газа в точке 1 перемещаются в положение 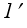навстречу потоку газа, а в газовой струе канала зарождается элемент звуковой поверхности, который условно изображен кривой  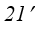на рис. 1. Дальнейшее понижение давления газа за каналом ведет к увеличению скорости в дозвуковой части потока и к достижению скорости газа в точке 3 слоя 3-3 местной скорости звука и критического давления 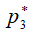. Так как 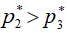, то разность давлений между слоями 2-2 и 3-3 в дозвуковой их части обусловит расширение газа в слое 2-2 навстречу потоку до тех пор, пока давление  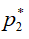в слое 2-2 не выровняется с давлением в слое 3-3. В результате этого параметры точки 2 переместятся в точку 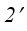, а параметры в точке 1 переместятся в точку 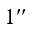. Причем смещение параметров в слое 2-2 по отношению к параметрам в слое 3-3 будет происходить одновременно с параметрами в слое 1-1 как единое целое, не нарушая равновесия между слоями 1-1 и 2-2, достигнутого ранее. Доля звуковой поверхности в газовой струе увеличится (условно изображена на рис. 1 кривой 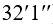). Дальнейшее понижение давления за каналом ведет к росту расхода газа через канал, однако темп роста расхода газа замедляется, так как звуковая доля потока увеличивается, а дозвуковая уменьшается, а прирост расхода газа через канал обеспечивается только дозвуковой частью потока. Скорость газа в слое (-1) - (-1) увеличивается и при некотором давлении 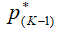 достигает значения, равного местной скорости звука. Поскольку давление 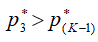, то разность давлений между слоями 3-3 и (K-1) - (K-1) в дозвуковой их части обусловит расширение газа в слое 3-3 навстречу потоку, пока давление 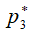не достигнет давления, равного в слое (K-1) - (K-1). Одновременно с расширением газа в слое 3-3 идет расширение газа и в слоях 2-2, 1-1 как единого целого. В результате этого звуковая поверхность сместится навстречу газовому потоку и займет новое положение, которое условно показано на рис. 1 кривой (K-1) 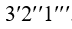. Дальнейшее понижение давления за каналом ведет к тому, что в пристенном слое газа K - K скорость газа достигает местной скорости звука и критического давления 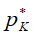. Звуковая поверхность сместится навстречу газовому потоку и займет новое положение, которое условно показано на рис. 1 кривой 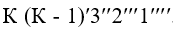. Эта звуковая поверхность опирается на края канала, и дальнейшее понижение давления за каналом не ведет к ее смещению навстречу потоку, так как понижение давления за каналом не может проникнуть внутрь канала за звуковую поверхность. Эта поверхность называется замкнутой звуковой поверхностью (ЗЗП). Расход газа через канал при этом достигает максимального значения, а звуковая поверхность максимально смещается внутрь канала навстречу потоку. Основной причиной несовпадения звуковой поверхности с выходным сечением канала является начальная неравномерность поля скоростей на выходе канала. По этой причине не может образоваться звуковая поверхность при одном каком-то давлении за каналом. Поверхность образуется последовательно и непрерывно по мере понижения давления газа за каналом. Происходит послойное «запирание» канала до тех пор, пока в пристенном слое газа не возникнут критические параметры. Это приведет к полному «запиранию» канала по расходу.

Для проверки работоспособности предложенной физической модели возникновения и развития звуковой поверхности в газовом потоке привлечем экспериментальные данные работы [2] по полю скоростей для трубы l/d = 49 и используем зависимость 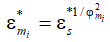 из работы [3], построим график рис. 2.

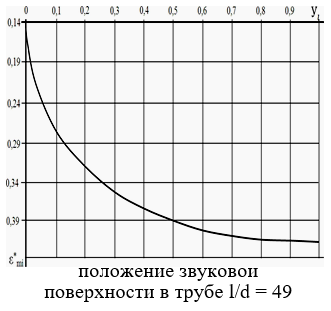
Начало координат графика поместим на стенки в выходном сечении канала. Ось абсцисс направим по радиусу канала, а ось ординат направим по стенке навстречу потоку. По оси абсцисс отложим относительные координаты газовых слоев в потоке 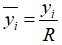,  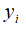 - расстояние от стенки R - радиус канала. По оси ординат отложим отношения критических давлений в газовых слоях канала .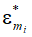

Полученная экспериментальная кривая фиксирует газодинамическое (параметрическое) положение звуковой поверхности в трубе l/d = 49. Видим, что кривая значительно сместилась внутрь канала, навстречу потоку, относительно выходного сечения канала. Из сравнения рис. 1 и рис. 2 следует, что экспериментальная кривая рис. 2 подтверждает физическую модель возникновения и развития звуковой поверхности в реальном газовом потоке цилиндрического канала.

Таким образом, представленная физическая модель возникновения и развития звуковой поверхности в неравномерном газовом потоке цилиндрического канала позволяет решить проблемы, возникающие при экспериментальном исследовании критических режимов истечения газа.

Неравномерность статического давления на звуковой поверхности

Расширение газа в цилиндрическом канале под действием сверхкритического перепада давления на начальном этапе идет по всему поперечному сечению канала. Статическое давление в поперечном сечении канала распределено равномерно. При достижении в первом слое газового потока критических параметров картина расширения газа в канале кардинально меняется. Критическое давление первого слоя, как бы ни понижали давление за каналом, остается неизменной величиной, поскольку нет условий для перехода скорости газа на сверхзвуковой режим течения. Критическое давление первого слоя является началом отсчета нового режима течения газа в канале. Начинается послойное плавное «запирание» канала по расходу по мере понижения давления за каналом. Это обусловлено начальной неравномерностью поля скоростей на выходе цилиндрического канала. Для того чтобы достичь критических параметров в каждом слое газового потока, необходимо увеличить скорость каждого слоя до звуковой скорости за счет потенциальной энергии давления этих слоев, поскольку после достижения в первом слое газового потока критических параметров в остальных слоях скорости газа дозвуковые. Причем в слоях газа, примыкающих к первому слою, разность между дозвуковыми и критическими скоростями этих слоев небольшая, то в слоях газа, примыкающих к пристенному слою, эта разность скоростей значительная. Так как дефицит скорости каждого слоя разный и восполняется за счет статического давления этого слоя, то и критическое давление на звуковой поверхности каждого слоя будет разным. Причем оно уменьшается от первого слоя к пристенному слою. Значение критического давления в каждом слое определяется формулой 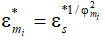,  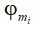- политропный коэффициент скорости i-го слоя газа. Скорость газа на звуковой поверхности определяется начальными параметрами газа перед каналом и не зависит от геометрии канала. Таким образом, расширение реального газа в цилиндрическом канале при сверхкритическом перепаде давлений начинается с неравномерным полем скоростей и равномерным полем статического давления в выходном сечении канала, а заканчивается с равномерным полем критических скоростей и неравномерным полем статического давления на звуковой поверхности канала.

Смещение звуковой поверхности в газовом потоке цилиндрического канала

При зарождении в газовом потоке элемента звуковой поверхности по радиусу канала появляется неравномерность давлений. Причем с уменьшением критического давления пристенного слоя эта неравномерность увеличивается. Перемещение критического давления предыдущего слоя газа навстречу потоку равно разности критических давлений между предыдущим и последующим слоями. Слой с меньшим критическим давлением смещает критическое давление слоя с большим давлением на величину, равную их разности. Согласно изложенной физической модели возникновения и развития звуковой поверхности (см. рис. 1), наибольшее смещение навстречу потоку будет иметь слой, где впервые в потоке возникло критическое давление газа. Наибольшей смещающей способностью обладает критическое давление пристенного слоя. Оно сдвигает критические давления всех предыдущих слоев на максимальную величину, но в каждом слое эта величина смещения будет различной, и определяется она разностью критических давлений данного и пристенного слоев. Определим максимальную разность критических давлений в газовом потоке по радиусу цилиндрического канала l/d = 49 с критическими параметрами 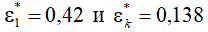  (см. рис. 2) по формуле

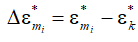, (1)

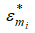где  и 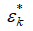− критическое отношение давлений в i-м и пристенном слоях газового потока соответственно.

Составим таблицу этих смещений

Таблица

Газодинамическое смещение звуковой поверхности

Это есть газодинамическое смещение звуковой поверхности, но есть необходимость получить и геометрическое (линейное) смещение звуковой поверхности навстречу потоку от выходного сечения канала. Для этого необходимо знать коэффициент пересчета газодинамического перемещения в геометрическое, то есть

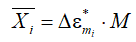 ,  (2)

где  ;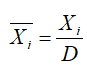

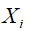− линейное максимальное смещение критического отношения давлений i-го слоя газа от выходного сечения канала навстречу потоку;

D − диаметр канала;

M − коэффициент пересчета.

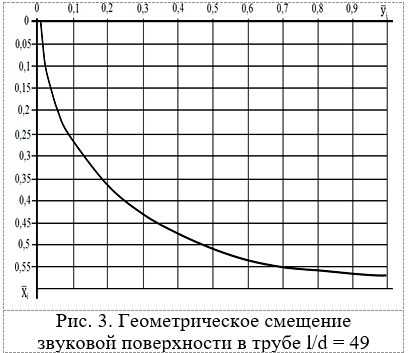
Анализ экспериментальных и расчетных данных показывает, что коэффициент пересчёта M = 2,015 для цилиндрического канала l/d = 49. Тогда, используя данные табл. и формулу (2), построим график максимального геометрического смещения ЗЗП в газовом потоке трубы l/d = 49. Из графика рис. 3 следует, что максимальное геометрическое смещение критического отношения давлений внутрь канала имеет первый слой газового потока. Остальные слои смещаются внутрь канала пропорционально разности критических отношений давлений i-го и пристенного слоев.

Таким образом, смещение звуковой поверхности навстречу потоку происходит под действием сил, обусловленных начальной неравномерностью поля скоростей на выходе канала.

Выводы

1. Представленная физическая модель возникновения и развития звуковой поверхности в неравномерном газовом потоке цилиндрического канала позволяет решить проблемы, возникающие при экспериментальном исследовании критических режимов истечения газа.
2. Расширение реального газа в цилиндрическом канале при сверхкритическом перепаде давлений начинается с неравномерным полем скоростей и равномерным полем статического давления в выходном сечении канала, а заканчивается с равномерным полем критических скоростей и неравномерным полем статического давления на звуковой поверхности канала.
3. Смещение звуковой поверхности навстречу потоку происходит под действием сил, обусловленных начальной неравномерностью поля скоростей на выходе канала.

1. Дейч М.Е. Техническая газодинамика / М.Е. Дейч. – М.: Энергия, 1974. – 592 с.
2. Дейч М.Е. Об особенностях течения газа на выходном участке трубы при сверхкритических перепадах давлений / М.Е. Дейч, В.В. Усанов, В.Д. Евдокимов, А.Е. Комаров // Теплоэнергетика. - 1979. − № 2. − С. 28 - 31.
3. Лухтура Ф.И. К вопросу об установившемся режиме истечения газа из осисимметричных отверстий и сопел / Ф.И. Лухтура // Вестник Приазовского государственного технического университета 2015г. Вып. 30. Т. 1 – С. 213-225.
4. Сиваков В.И. Определение критических параметров реального (вязкого) газового потока по известному полю скоростей на выходе канала. Определение поля скоростей по известному критическому отношению давлений в пристенном слое газового потока канала / В.И. Сиваков // Научный аспект № 5 – 2024 (электронный ресурс)